《数据结构强化笔记》续篇——常用算法代码模板,以C++为算法题解主语言,兼以部分Java版模板。
Ultimate Solutions: A comprehensive collection of solutions for programming challenges from LeetCode, PAT (Programming Ability Test), and other coding platforms.
GitHub:github.com/hyperplasma/Ultimate-Solutions
Gitee:gitee.com/hyperplasma/Ultimate-Solutions
0 算法时间复杂度分析
由数据范围反推算法时间复杂度。
对于时间限制为[1\text{s},2\text{s}]的题目,C++代码中的操作次数应控制在[10^7,10^8]为最佳。
| 数据范围 | 时间复杂度 | 算法 |
|---|---|---|
n≤30 |
指数级 | dfs+剪枝、状态压缩dp |
n≤100 |
O(n^3) |
floyd、dp、高斯消元 |
n≤1000 |
O(n^2),O(n^2\log n) |
dp、二分、朴素dijkstra、朴素prim、Bellman-Ford |
n≤10^4 |
O(n\sqrt n) |
块状链表、分块 |
n≤10^5 |
O(n\log n) |
sort、线段树、树状数组、set/map、heap、dijkstra+heap、spfa |
n≤10^6 |
① O(n)② 常数比较小的 O(n\log n) |
① 单调队列、hash、双指针、bfs、并查集、kmp、AC自动机 ② sort、树状数组、heap、dijkstra+heap、spfa |
n≤10^7 |
O(n) |
双指针、kmp、AC自动机、线性筛素数 |
n≤10^9 |
O(\sqrt n) |
判断质数 |
n≤10^{18} |
O(\log n) |
欧几里得算法、快速幂、数位dp |
1 基础算法
排序、二分、高精度、前缀和与差分、位运算、双指针、离散化、区间合并
1.1 排序
标准库排序函数:
- C++:
std::sort(begin, end, cmp) - Java:
Arrays.sort(arr, [fromIndex, toIndex])、Arrays.sort(arr, (a, b) -> b - a)
元素交换:
- C++:直接使用标准库函数
std::swap(a, b) - Java:
- 交换列表集合中两元素可使用
Collections.swap(list, index1, index2) - 自行编写以下方法实现交换数组中两元素(若无特殊定义,本文Java模板中如有出现调用
swap(arr, i, j),均指使用本方法):
- 交换列表集合中两元素可使用
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}1.1.1 直接插入排序
本文保证各种数组长度常量(
N)足够大
C++
int n;
int q[N]; // q[0 ... n-1]
void insert_sort() {
for (int i = 1; i < n; i++) {
for (int j = i; j >= 1 && q[j] > q[j - 1]; j--) {
swap(q[j], q[j - 1]);
}
}
}Java
public static void insertSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
for (int j = i; j >= 1 && arr[j] > arr[j - 1]; j--) {
swap(arr, j, j - 1);
}
}
}1.1.2 快速排序
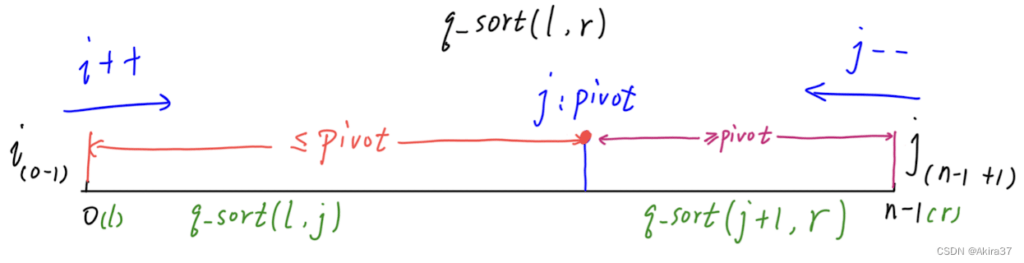
- 确定枢轴:通常从
q[l]、q[l + r >> 1]、q[r]之中任选一个 - 划分子区间:双指针
i、j初始位于待排区间两侧外,先i后j相向而行,最终使得左右子区间q[l ... j]、q[j+1 ... r]左小右大 - 递归排序左右子区间(该写法左子区间右端点必须为
j)
C++
int q[N]; // q[l ... r]
void quick_sort(int l, int r) {
if (l >= r) return; // 只剩一个数或没有数了则不排序
int x = q[l + r >> 1]; // 枢轴(可选 q[l]、q[l + r >> 1]、q[r])
int i = l - 1, j = r + 1; // 双指针初始位于两侧外(追加1偏移量)
while (i < j) { // 进行一轮划分操作
do i++; while (q[i] < x);
do j--; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(l, j); // 左子区间右端点必须为j
quick_sort(j + 1, r);
}Java
/* arr[l ... r] */
public static void quickSort(int[] arr, int l, int r) {
if (l >= r) return;
int x = arr[l + (r - l) / 2]; // 枢轴(选择中间元素)
int i = l - 1, j = r + 1; // 双指针初始位于两侧外(追加1偏移量)
while (i < j) {
do i++; while (arr[i] < x);
do j--; while (arr[j] > x);
if (i < j) swap(arr, i, j);
}
quickSort(arr, l, j); // 左子区间右端点必须为j
quickSort(arr, j + 1, r);
}1.1.3 归并排序
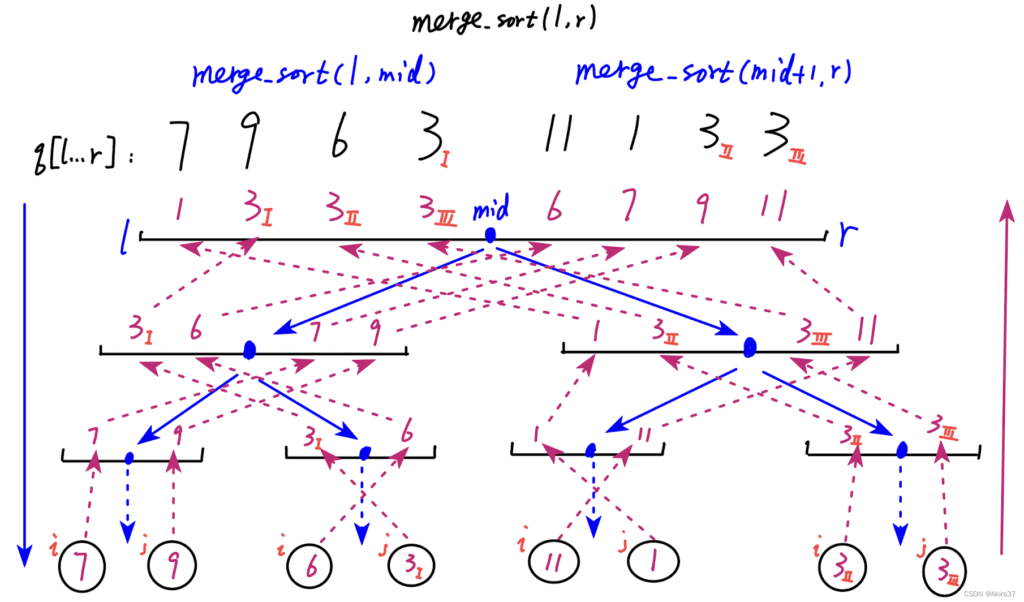
- 确定分界点:
mid = l + r >> 1 - 递归排序左右子区间
- 归并左右子区间为有序子区间:挑出两者较小值,相等则优先归并
q[i],使得排序稳定
C++
int q[N]; // q[l ... r]
int tmp[N]; // 辅助数组tmp临时存放新区间
void merge_sort(int l, int r) {
if (l >= r) return; // 只剩一个数或没有数了则不排序
int mid = l + r >> 1; // 确认分界点:左[l, mid]、右[mid + 1, r]
merge_sort(l, mid);
merge_sort(mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r) // 归并左右子区间为有序子区间:挑出两者较小值
if (q[i] <= q[j]) {
tmp[k++] = q[i++]; // 相等则优先归并q[i],否则排序不稳定
} else {
tmp[k++] = q[j++];
}
while (i <= mid) {
tmp[k++] = q[i++];
}
while (j <= r) {
tmp[k++] = q[j++];
}
for (i = l, j = 0; i <= r; ++i, ++j) {
q[i] = tmp[j]; // 将tmp[0 ... r-l+1]复制给q[l ... r]
}
}Java
/* arr[l ... r] */
public static void mergeSort(int[] arr, int l, int r) {
if (l >= r) return;
int mid = l + r >> 1;
mergeSort(arr, l, mid); // 递归排序左半部分
mergeSort(arr, mid + 1, r); // 递归排序右半部分
int[] temp = new int[r - l + 1]; // 辅助数组
int i = l, j = mid + 1, k = 0; // 初始化指针
while (i <= mid && j <= r) { // 归并左右子区间为有序子区间
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
// 并入区间剩余元素
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= r) {
temp[k++] = arr[j++];
}
// 将排序后的结果复制回原始数组
for (i = l, j = 0; i <= r; i++, j++) {
arr[i] = temp[j];
}
}1.2 二分查找
整数二分:AcWing 789. 数的范围
- 中点将区间划分出左右两子区间
- 判断中间点是否满足某侧区间的性质
check(mid),查找○边界,目标在○区间,检测○区间性质。易知该种写法条件检测始终为"≥"或"≤",对应下文记号ge()(greater_equal)、le()(less_equal),对比目标和中点的位置关系即可得出条件检测函数 - 返回所检测的○区间的端点○
当查找右边界时中点应为
l + r + 1 >> 1,简记:有("右") 加必有("右") 减
浮点数二分:类似整数二分的查找左边界,常写作f(mid) >= target的形式。解唯一,无需处理边界。要注意浮点精度问题。
C++
int target;
/* 查找左边界,即第一个满足条件的元素下标 (lower_bound) */
int bsearch_l(int l, int r) {
while (l < r) {
int mid = l + r >> 1;
if (ge(mid, target)) {
r = mid; // 目标在左,mid所指>=目标:带mid去左边[l, mid]
} else {
l = mid + 1; // 否则去右边 [mid + 1, r]
}
}
return l;
}
/* 查找右边界,即最后一个满足条件的元素下标 (upper_bound的前驱) */
int bsearch_r(int l, int r) {
while (l < r) {
int mid = l + r + 1 >> 1; // 有(“右”)加必有(“右”)减
if (le(mid, target)) {
l = mid; // 目标在右,mid所指<=目标:带mid去右边[mid, r]
} else {
r = mid - 1; // 否则去左边: [l, mid - 1]
}
}
return r;
}
/* 浮点数二分 */
int bsearch_f(double l, double r) {
const double eps = 1e-8; // 精度,视题目而定
while (r - l > eps) {
double mid = (l + r) / 2;
if (ge(mid, target)) {
r = mid; // 目标在左,mid所指>=目标。注意浮点关系运算精度问题
} else {
l = mid; // 边界均无需+1或-1
}
}
return l;
}Java
static int target;
/* 查找左边界,即第一个满足条件的元素下标 (lower_bound) */
public static int binarySearchL(int l, int r) {
while (l < r) {
int mid = l + r >> 1; // 计算中点值
if (ge(mid, target)) {
r = mid; // 如果中点值符合条件,则继续在左边查找
} else {
l = mid + 1; // 否则在右边查找
}
}
return l; // 返回左边界
}
/* 查找右边界,即最后一个满足条件的元素下标 (upper_bound的前驱) */
public static int binarySearchR(int l, int r) {
while (l < r) {
int mid = l + r + 1 >> 1; // 计算中点值,向右偏移
if (le(mid, target)) {
l = mid; // 如果中点值符合条件(≤),则继续在右边查找
} else {
r = mid - 1; // 否则在左边查找
}
}
return r; // 返回右边界
}
/* 浮点数二分 */
public static double binarySearchF(double l, double r) {
final double eps = 1e-8; // 精度,视题目而定
while (r - l > eps) {
double mid = (l + r) / 2; // 计算中点值
if (ge(mid, target)) {
r = mid; // 目标在左边,更新右边界
} else {
l = mid; // 否则更新左边界
}
}
return l; // 返回左边界,即为目标值的估计
}1.3 高精度运算
除了存储大整数外还可用于任意进制数的表示与运算,只需将10改为其他进制即可。
C++
常使用变长数组std::vector<int>或字符串std::string存储大整数及其属性,低位存于低位。
int base = 10;
/* 高精度加法:C = A + B, A >= 0, B >= 0 */
vector<int> add(vector<int> &A, vector<int> &B) {
if (A.size() < B.size()) return add(B, A);
vector<int> C;
int t = 0; // 进位
for (int i = 0; i < A.size(); i++) {
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % base);
t /= base;
}
if (t) {
C.push_back(t); // 存入最后的进位
}
return C;
}
/* 比较两个高精度整数的大小,返回A - B的符号 */
int cmp(vector<int> &A, vector<int> &B) {
if (A.size() > B.size()) return 1; // 优先比较长度
else if (A.size() < B.size()) return -1;
for (int i = A.size() - 1; i >= 0; i--) // 从高位起逐位比较
if (A[i] > B[i]) return 1;
else if (A[i] < B[i]) return -1;
return 0;
}
/* 高精度减法:C = A - B, A >= B, A >= 0, B >= 0 */
vector<int> sub(vector<int> &A, vector<int> &B) {
vector<int> C;
int t = 0; // 借位
for (int i = 0; i < A.size(); i++) {
t = A[i] - t; // 成为本轮的被减数
if (i < B.size()) t -= B[i]; // 先直接相减,t<0则说明需借位
C.push_back((t + base) % base); // 若t<0,则存的是借位后的差;否则正常存差
if (t < 0) { // 判断是否需借位
t = 1;
} else {
t = 0;
}
}
while (C.size() > 1 && C.back() == 0) {
C.pop_back(); // 去除前导0(结果为0则保留1位)
}
return C;
}
/* 高精度乘低精度:C = A * b, A >= 0, b >= 0 */
vector<int> mul(vector<int> &A, int b) {
vector<int> C;
int t = 0; // 进位
for (int i = 0; i < A.size() || t; i++) { // 自动处理最后剩余进位(i>=size但t>0的情形)
if (i < A.size()) t += A[i] * b;
C.push_back(t % base);
t /= base;
}
while (C.size() > 1 && C.back() == 0) {
C.pop_back(); // b为0时,需去除前导0
}
return C;
}
/* 高精度除以低精度:A / b = C ... r, A >= 0, b > 0 */
vector<int> div(vector<int> &A, int b, int &r) {
vector<int> C;
r = 0; // 余数
for (int i = A.size() - 1; i >= 0; i--) { // 从最高位开始除
r = r * base + A[i];
C.push_back(r / b); // 暂时将高位存于低位
r %= b;
}
reverse(C.begin(), C.end()); // 逆转后即为正常存储形式
while (C.size() > 1 && C.back() == 0) {
C.pop_back();
}
return C;
}Java
可直接用ArrayList甚至数组存储,具体要点类似C++;亦可直接使用内置大数类BigInteger存储。
static int base = 10; // 进制
/* 高精度加法 C = A + B, A >= 0, B >= 0 */
public static ArrayList<Integer> add(ArrayList<Integer> A, ArrayList<Integer> B) {
if (A.size() < B.size()) {
return add(B, A);
}
ArrayList<Integer> C = new ArrayList<>();
int t = 0; // 进位
for (int i = 0; i < A.size(); i++) {
t += A.get(i);
if (i < B.size()) {
t += B.get(i);
}
C.add(t % base);
t /= base;
}
if (t > 0) {
C.add(t); // 存入最后的进位
}
return C;
}
/* 比较两个高精度整数的大小,返回A - B的符号 */
public static int cmp(ArrayList<Integer> A, ArrayList<Integer> B) {
if (A.size() > B.size()) {
return 1; // 优先比较长度
} else if (A.size() < B.size()) {
return -1;
}
for (int i = A.size() - 1; i >= 0; i--) // 从高位起逐位比较
if (A.get(i) > B.get(i)) {
return 1;
} else if (A.get(i) < B.get(i)) {
return -1;
}
return 0;
}
/* 高精度减法 C = A - B, A >= B, A >= 0, B >= 0 */
public static ArrayList<Integer> sub(ArrayList<Integer> A, ArrayList<Integer> B) {
ArrayList<Integer> C = new ArrayList<>();
int t = 0; // 借位
for (int i = 0; i < A.size(); i++) {
t = A.get(i) - t; // 成为本轮的被减数
if (i < B.size()) {
t -= B.get(i); // 先直接相减,t<0则说明需借位
}
C.add((t + base) % base); // 若t<0,则存的是借位后的差;否则正常存差
if (t < 0) { // 判断是否需借位
t = 1;
} else {
t = 0;
}
}
while (C.size() > 1 && C.get(C.size() - 1) == 0) {
C.remove(C.size() - 1); // 去除前导0(结果为0则保留1位)
}
return C;
}
/* 高精度乘法 C = A * b, A >= 0, b >= 0 */
public static ArrayList<Integer> mul(ArrayList<Integer> A, int b) {
ArrayList<Integer> C = new ArrayList<>();
int t = 0; // 进位
for (int i = 0; i < A.size() || t > 0; i++) { // 自动处理最后剩余进位(i>=size但t>0)
if (i < A.size()) {
t += A.get(i) * b;
}
C.add(t % base);
t /= base;
}
while (C.size() > 1 && C.get(C.size() - 1) == 0) {
C.remove(C.size() - 1); // b为0时,需去除前导0
}
return C;
}
/* 高精度除法 A / b = C ... r, A >= 0, b > 0 */
public static ArrayList<Integer> div(ArrayList<Integer> A, int b, int[] r) {
ArrayList<Integer> C = new ArrayList<>();
r[0] = 0; // 余数
for (int i = A.size() - 1; i >= 0; i--) { // 从最高位开始除
r[0] = r[0] * base + A.get(i);
C.add(r[0] / b); // 暂时将高位存于低位
r[0] %= b;
}
Collections.reverse(C); // 逆转后即为正常存储形式
while (C.size() > 1 && C.get(C.size() - 1) == 0) {
C.remove(C.size() - 1);
}
return C;
}1.4 前缀和、差分
以下前缀和与差分数组必须从下标1开始存储
1.4.1 一维前缀和
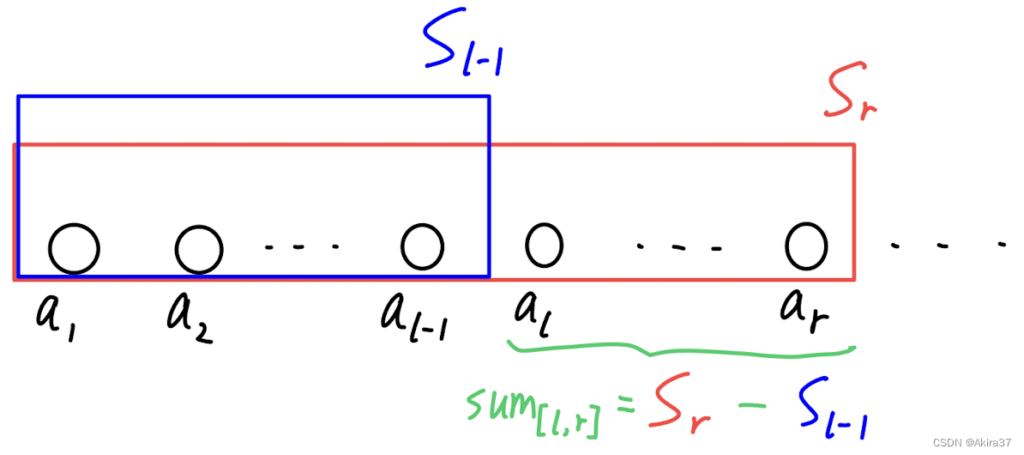
对于数列a[1], a[2], ... , a[n],规定a[i]的前缀和为前i个数的和:s[i] = a[1] + a[2] + ... + a[i] (i >= 1)
求法:s[0] = 0, s[i] = s[i - 1] + a[i] (i >= 1)
应用:求下标区间[l,\ r]上的片段和s[r] - s[l - 1]
C++
int n;
int a[N], s[N]; // [1 ... n]
/* 初始化前缀和数组 */
void init() {
for (int i = 1; i <= n; i++) {
s[i] = s[i - 1] + a[i];
}
}
/* 求下标区间[l, r]上的片段和 */
int get(int l, int r) {
return int sum = s[r] - s[l - 1]; // sum = a[l] + ... + a[r]
}Java
static int n;
static int[] a; // [1 ... n]
static int[] s; // [1 ... n]
/* 初始化前缀和数组 */
public static void init() {
for (int i = 1; i <= n; i++) {
s[i] = s[i - 1] + a[i];
}
}
/* 求下标区间[l, r]上的片段和 */
public static int get(int l, int r) {
return s[r] - s[l - 1];
}1.4.2 二维前缀和
对于n * m的矩阵a[n][m],规定a[i][j]的二维前缀和s[i][j]为元素a[i][j]左上角所有元素的和。
求法:s[0][j] = s[i][0] = s[0][0] = 0, s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j] (i, j >= 1)
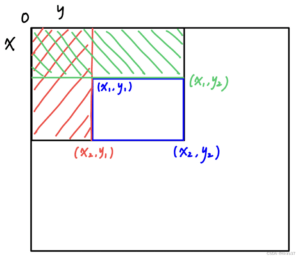
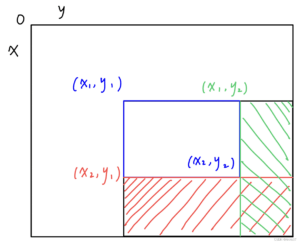
应用:求下图以(x1, y1)为左上角、(x2, y2)为右下角的子矩阵(含边界)上的片段和,只需将整块左上矩形面积减去红、绿区域(不含待求区域边界)面积再补上多减去的重叠区域面积,即为S = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]
C++
int n, m;
int a[N][N], s[N][N]; // [1 ... n][1 ... m]
/* 初始化前缀和数组 */
void init() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
}
}
/* 求以(x1, y1)为左上角、(x2, y2)为右下角的子矩阵(含边界)上的片段和 */
int get(int x1, int y1, int x2, int y2) {
return s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
}Java
static int n;
static int m;
static int[][] a; // [1 ... n][1 ... m]
static int[][] s; // [1 ... n][1 ... m]
/* 初始化前缀和矩阵 */
public static void init() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
}
}
}
/* 求以(x1, y1)为左上角、(x2, y2)为右下角的子矩阵(含边界)上的片段和 */
public static int get(int x1, int y1, int x2, int y2) {
return s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
}1.4.3 一维差分
由数组a[1], a[2], ... ,a[n]构造差分数组b[1], b[2], ... , b[n],使得a[i] = b[1] + b[2] + ... + b[i],b[i] = a[i] - a[i - 1]
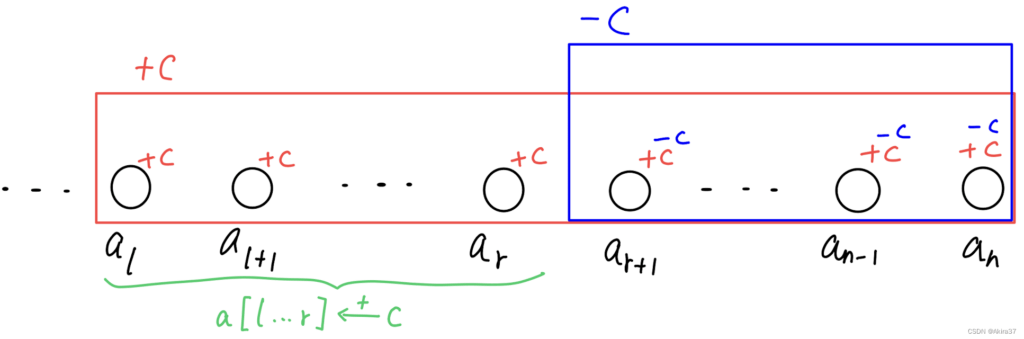
应用:给区间[l, r]上所有数加上C,时间复杂度O(1)。方法如下
- 给
b[l]加上C,使得a[l], a[l + 1], ... , a[n]均加上了C - 给
b[r + 1]减去C,使得a[r + 1], a[r + 2], ... , a[n]均减去了本不应加的C
对于原差分数组的初始化亦可采用上述操作,赋值
a[i]即相当于给区间[i, i]加上a[i]
C++
int n;
int a[N], b[N]; // [1 ... n]
/* 给区间[l, r]上所有数加上c */
void insert(int l, int r, int c) {
b[l] += c;
b[r + 1] -= c;
}
/* 初始化差分数组 */
void init() {
for (int i = 1; i <= n; i++) {
insert(i, i, a[i]);
}
}
/* 将操作过的差分数组变为原数组(前缀和与差分互为逆运算) */
void revert() {
for (int i = 1; i <= n; i++) {
b[i] += b[i - 1];
}
}Java
static int n;
static int[] a; // [1 ... n]
static int[] b; // [1 ... n]
/* 给区间[l, r]上所有数加上c */
public static void insert(int l, int r, int c) {
b[l] += c;
b[r + 1] -= c;
}
/* 初始化差分数组 */
public static void init() {
for (int i = 1; i <= n; i++) {
insert(i, i, a[i]);
}
}
/* 将操作过的差分数组变为原数组(前缀和与差分互为逆运算) */
public static void revert() {
for (int i = 1; i <= n; i++) {
b[i] += b[i - 1];
}
}1.4.4 二维差分
参考一维差分与二维前缀和,差分矩阵中每个数都蕴含于其右下矩阵中的每个数。
操作:给下图以(x1, y1)为左上角、(x2, y2)为右下角的子矩形(含边界)加上C,只需给整个右下角加C,给红、绿区域各减C,最后再给重叠区域加上多减的C即可
对于原差分矩阵初始化操作亦可采用上述操作,参考一维差分
C++
int n, m;
int a[N][N], b[N][N]; // [1 ... n][1 ... m]
/* 给以(x1, y1)为左上角、(x2, y2)为右下角的子矩阵(含边界)加上c */
void insert(int x1, int y1, int x2, int y2, int c) {
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
/* 初始化差分矩阵 */
void init() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
insert(i, j, i, j, a[i][j]);
}
}
}
/* 将操作过的差分矩阵变为原矩阵:求差分矩阵的前缀和 */
void revert() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
}
}
}Java
static int n;
static int m;
static int[][] a; // [1 ... n][1 ... m]
static int[][] b; // [1 ... n][1 ... m]
/* 给以(x1, y1)为左上角、(x2, y2)为右下角的子矩阵(含边界)加上c */
public static void insert(int x1, int y1, int x2, int y2, int c) {
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
/* 初始化差分矩阵 */
public static void init() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
insert(i, j, i, j, a[i][j]);
}
}
}
/* 将操作过的差分矩阵变为原矩阵:求差分矩阵的前缀和 */
public static void revert() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
}
}
}1.5 位运算
n的二进制表示中第k位数字:n >> k & 1(先把第k位数字移到最后一位,再看个位是几,即和1做按位与运算)lowbit(x) = x & -x:返回x的最后一位1
C++
/* 返回x的最后一位1 */
int lowbit(int x) {
return x & -x; // -x = ~x + 1
}
/* 输出整数x的二进制表示(31位)*/
void println_binary(int x) {
for (int i = 0; i < 31; i++) {
printf("%d", x >> i & 1);
}
}
/* 统计x的二进制表示中有几位1 */
int count_ones(int x) {
int cnt = 0;
while (x) {
x -= lowbit(x);
cnt++;
}
return cnt;
}Java
/* 返回x的最后一位1 */
public static int lowbit(int x) {
return x & -x; // -x = ~x + 1
}
/* 输出整数x的二进制表示(31位)*/
public static void printlnBinary(int x) {
for (int i = 0; i < 31; i++) {
System.out.print(x >> i & 1);
}
}
/* 统计x的二进制表示中有几位1 */
public static int countOnes(int x) {
int cnt = 0;
while (x != 0) {
x -= lowbit(x);
cnt++;
}
return cnt;
}1.6 双指针算法
常见的双指针问题可大致分为以下两类:
- 对于一个序列,用两个指针维护一段区间
- 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
朴素双指针O(n^2):
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
// ...
}
}优化双指针O(n):
/* i为子序列右端点,j为左端动点 */
for (int i = 0, j = 0; i < n; i++) {
while (j < i && check(i, j)) {
// ...
j++;
}
// ...
}/* i为子序列左端点,j为动态右端动点 */
for (int i = 0; i < n;) {
int j = i;
while (j < n && check(i, j)) {
// ...
j++;
}
// ...
i = j + 1; // 将i直接移至j附近
}1.7 离散化
离散化(Discretization):高度分散的整数 → 0, 1, 2, ..., n-1或1, 2, ..., n
C++
vector<int> alls; // 存储所有待离散化的值
/* 离散化操作(保序) */
void init() {
sort(alls.begin(), all.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), all.end()); // 去重
}
/* 根据离散化的值k获取原来的值x */
int get(k) {
return alls[k];
}
/* 二分求出x对应的离散化的值 */
int find(int x) {
int l = 0, r = alls.size() - 1;
while (l < r) { // 找到第1个大于等于x的位置(唯一)
int mid = l + r >> 1;
if (alls[mid] >= x) {
r = mid;
} else {
l = mid + 1;
}
}
return r + 1; // 这里+1是为了映射到1, 2, ..., alls.size()
}Java
static List<Integer> alls = new ArrayList<>(); // 存储所有待离散化的值
/* 初始化离散化列表(保序) */
public static void init() {
Collections.sort(alls); // 将所有值排序
alls = new ArrayList<>(new HashSet<>(alls)); // 去重
}
/* 根据离散化的值k获取原来的值x */
public static int get(int k) {
return alls.get(k);
}
/* 二分求出x对应的离散化的值 */
public static int find(int x) {
int l = 0, r = alls.size() - 1;
while (l < r) { // 找到第一个大于等于x的位置(唯一)
int mid = (l + r) >> 1;
if (alls.get(mid) >= x) {
r = mid;
} else {
l = mid + 1;
}
}
return r + 1; // 这里+1是为了映射到1, 2, ..., alls.size()
}1.8 区间合并
- 先将所有区间按左端点大小排序
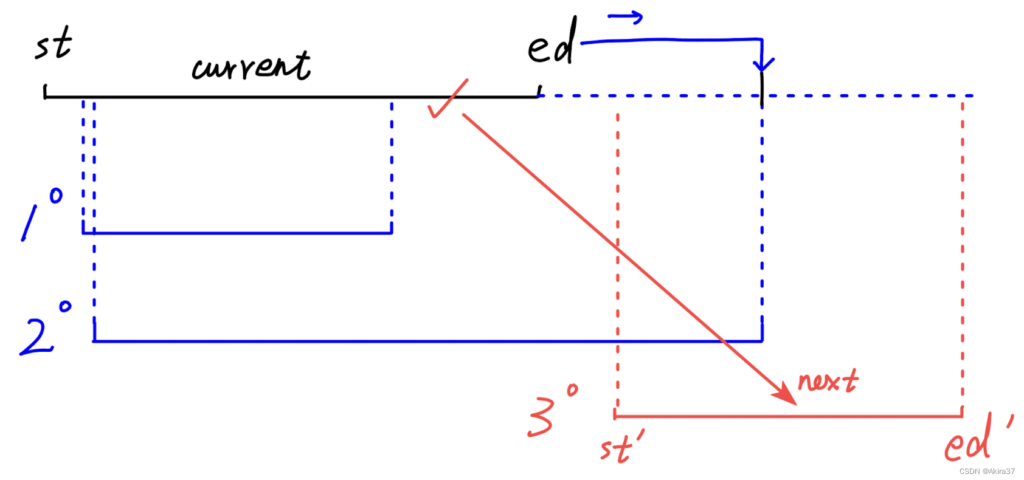
- 当前维护区间与下一区间之间分三种情况:包含、有交集(含端点)、无交集
- 包含:无需操作(实为有交集的特殊情况)
- 有交集:更新当前区间右端点为较大的即可,继续维护
- 无交集:结束维护当前区间并保存,更新为下一区间
- 迭代结束后保存当前维护区间
C++
typedef pair<int, int> PII; // <st, ed>
/* 合并区间 */
vector<PII> merge(vector<PII> &segs) {
vector<PII> res;
sort(seg.begin(), seg.end()); // 默认优先按first(左端点大小)排序
int st = -INF, ed = -INF; // 当前维护区间(初始化为负无穷)
for (auto &seg : segs) {
if (ed < seg.first) { // 若与当前维护区间无交集
if (st != -INF) {
res.push_back({st, ed}); // 当前区间结束维护并保存
}
st = seg.first; // 转移至此区间
ed = seg.second;
} else {
ed = max(ed, seg.second); // 有交集则比较右端点即可,继续维护
}
}
if (st != -INF) {
res.push_back({st, ed}); // 保存最后一个区间
}
return res;
}Java
/* 合并区间:segs中每个元素表示一段区间,int[0]表示左端点,int[1]表示右端点 */
public static List<int[]> merge(List<int[]> segs) {
List<int[]> res = new ArrayList<>();
segs.sort(Comparator.comparingInt(a -> a[0])); // 按左端点大小排序
int st = Integer.MIN_VALUE, ed = Integer.MIN_VALUE; // 当前维护区间(初始化为负无穷)
for (int[] seg : segs) {
if (ed < seg[0]) { // 若与当前维护区间无交集
if (st != Integer.MIN_VALUE) {
res.add(new int[]{st, ed}); // 当前区间结束维护并保存
}
st = seg[0]; // 转移至此区间
ed = seg[1];
} else {
ed = Math.max(ed, seg[1]); // 有交集则比较右端点
}
}
if (st != Integer.MIN_VALUE) {
res.add(new int[]{st, ed}); // 保存最后一个区间
}
return res;
}2 数据结构
链表、栈、队列、单调队列、模式匹配、Trie树、并查集、堆、哈希
2.1 链表
用链式前向星(静态链表)实现链表的定义、遍历与增删改查。
2.1.1 单链表
无头单链表。元素结点地址idx从0开始分配,表尾空指针记为-1。

C++
int head, e[N], ne[N], idx;
// head为无头单链表的头指针
// e[i]存储结点i的值
// ne[i]指向结点i的后继
// idx为分配给结点的"地址"
/* 初始化 */
void init() {
head = -1; // 头指针初始为-1
idx = 0; // 这里设定第1个插入的结点在0号下标
}
/* 头插一个数x */
void insert_head(int x) {
e[idx] = x;
ne[idx] = head;
head = idx++; // 后继为开始结点
}
/* 在结点k之后插入一个数x */
void insert(int k, int x) {
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx++; // 后继为k的后继
}
/* 删除头结点(需保证链表非空) */
void remove_head() {
head = ne[head];
}
/* 删除结点k之后的结点 */
void remove(int k) {
ne[k] = ne[ne[k]]
}
/* 遍历整条链表 */
for (int i = head; ~i; i = ne[i]) {
int u = e[i];
// ...
}Java
/* 单链表结点 */
class ListNode {
int val;
ListNode next;
ListNode() {
}
ListNode(int val) {
this.val = val;
}
ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
}
/* 翻转链表 */
public static ListNode reverse(ListNode head) {
ListNode cur = head, pre = null;
while (cur != null) {
ListNode nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
}
return pre;
}
/* 快慢指针,寻找环 */
public static ListNode findMid(ListNode head) {
ListNode fast = head, slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}2.1.2 双链表
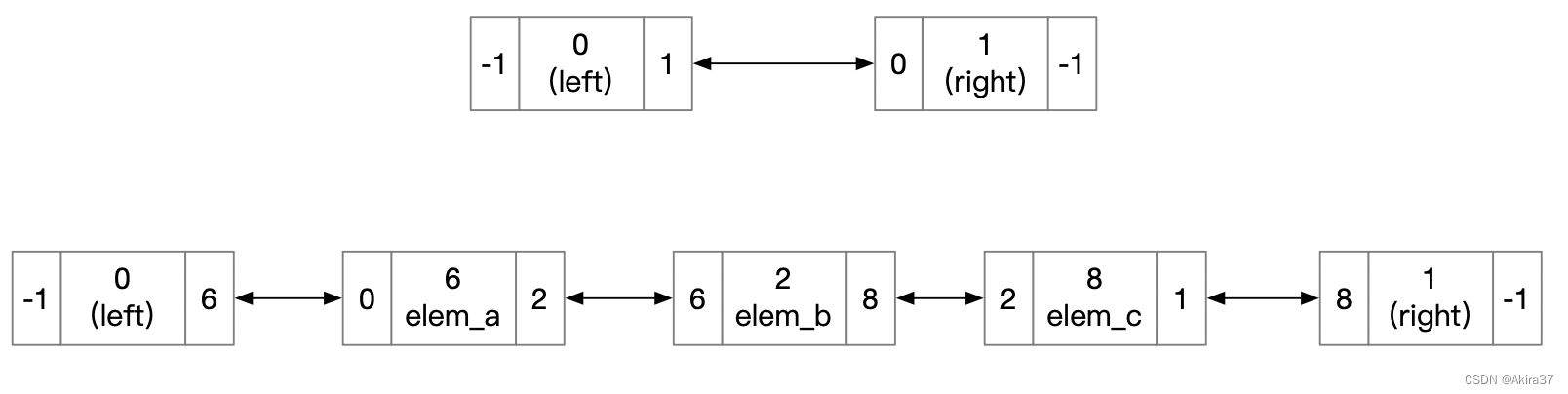
带头循环双链表。规定0为头结点/左端点,只有后继;1为尾结点/右端点,只有前驱。元素结点地址idx从2开始分配,每个元素结点都不含空指针。常用于实现双端队列。
对于删除操作,为避免繁杂通常不直接将结点移出链表,而是通过开bool数组
st[]标记结点来实现逻辑删除,st[i]记录结点i是否被删除。
为避免额外时间开销,本文大部分数据结构均采用此删除方法。
C++
int e[N], l[N], r[N], idx;
// l[i]、r[i]分别指向结点i的前驱、后继
// 特殊规定:0为头结点/左端点,只有后继;1为尾结点/右端点,只有前驱
/* 初始化 */
void init() {
r[0] = 1, l[1] = 0; // 左右端点分别指向对方
idx = 2; // 第1个结点从下标2开始存储
}
/* 在结点k的右边插入一个数x */
void insert_r(int k, int x) {
e[idx] = x;
l[idx] = k; // 前驱为k
r[idx] = r[k]; // 后继为k的后继
l[r[k]] = idx; // k后继的前驱、k的后继(须最后修改)即为该结点
r[k] = idx++;
}
/* 在结点k的左边插入一个数x */
void insert_l(int k, int x) {
insert_r(l[k], x); // 等价于在结点k的前驱(l[k])的右边插入
}
/* 删除结点k */
void remove(int k) {
l[r[k]] = l[k];
r[l[k]] = r[k];
}
/* 遍历整条链表 */
for (int i = r[0]; i != 1; i = r[i]) {
int u = e[i];
// ...
}2.2 栈与队列
2.2.1 栈
FILO。手工数组建栈可以实现随机存取或遍历栈内元素,若无此需求可直接使用std::stack。
C++
int stk[N], tt = -1;
// stk[0 ... N-1]
// 栈顶指针tt初始化为-1
/* 栈顶入栈一个数 */
void push(int x) {
stk[++tt] = x;
}
/* 栈顶出栈一个数 */
void pop() {
tt--;
}
/* 栈顶的值 */
int top() {
return stk[tt];
}
/* 判断栈是否为空 */
bool empty() {
return tt != -1;
}2.2.2 非循环队列
FIFO。手工建立的非循环队列中元素不会被覆盖,由此可以实现对队内历史元素的遍历与随机存取,或根据指针判断某些性质(如拓扑序列)。若无此需求,可使用std::queue、std::deque或std::list快速实现各种队列。
C++
int q[N], hh = 0, tt = -1;
// q[0 ... N-1]
// 队头初始为0, 队尾初始和栈顶一样为-1
/* 队尾入队一个数 */
void push(int x) {
q[++tt] = x;
}
/* 队头出队一个数 */
void pop() {
hh++;
}
/* 队头/队尾的值 */
int front() {
return q[hh];
}
int back() {
return q[tt];
}
/* 判断队列是否为空 */
bool empty() {
return hh <= tt;
}2.2.3 循环队列
常用于手动实现输入/输出限制的双端队列。
C++
int q[N], hh = 0, tt = 0;
// q[0 ... N-1]
// 队头和队尾指针初始均为0
/* 队尾入队一个数 */
void push(int x) {
q[tt++] = x;
if (tt == N) tt = 0;
}
/* 队头出队一个数 */
void pop() {
hh++;
if (hh == N) hh = 0;
}
/* 队头/队尾的值 */
int front() {
return q[hh];
}
int back() {
return q[tt];
}
/* 判断队列是否为空 */
bool empty() {
return hh != tt;
}2.2.4 单调栈(最近极值查找)
核心思想:及时弹出必不会作为答案的数,使得容器内各所指元素始终单调。
常见模型:找出数列中每个数左边离它最近的比它大/小的数。
【例】输出数组a[1 ... n]中每个数左边离它最近的比它小的数,不存在则输出-1(若想求大,只需改变判定弹出的不等号即可):
C++
int n, a[N]; // a[1 ... n]
int stk[N], tt = -1; // 栈中存储数组元素下标
// 思想:若a[x] >= a[y] (x < y),则a[x]必不会是任何一数的答案,可直接剔除
void print_nearest_mins() {
for (int i = 0; i < n; i++) { // 双指针算法,i是子区间右端点
while (tt != -1 && a[stk[tt]] >= a[i]) {
tt--; // 弹出既大又"远"的数
}
if (tt != -1) {
printf("%d ", a[stk[tt]]);
} else {
printf("-1 ");
}
stk[++tt] = i;
}
}2.2.5 单调队列(滑动窗口)
核心思想同单调栈。容器为输入限制的双端队列。
常见模型:找出滑动窗口中的最大值/最小值。
【例】设数组a[1 ... n]中的滑动窗口长度为k,输出滑动窗口每次前移时窗口内的最小值(若想求大,只需改变判定弹出的不等号即可):
C++
int n, a[N]; // a[1 ... n]
int k; // 滑动窗口的长度
int q[N], hh = 0, tt = -1; // 队列(双端队列)中存储数组元素下标
// 思想:同单调栈,且应输出的最值在队头(单调)
void print_window_mins() {
for (int i = 0; i < n; i++) { // 双指针算法,i是子区间右端点
while (hh <= tt && i - k + 1 > q[hh]) {
hh++; // 判断队头是否滑出窗口
}
while (hh <= tt && a[q[tt]] >= a[i]) {
tt--; // 同单调栈,队尾弹出既大又"远"的数
}
q[++tt] = i; // 先将i从队尾入队
if (i + 1 >= k) {
printf("%d ", a[q[hh]]); // 当窗口长度达到要求时才输出
}
}
}2.3 字符串
字符串的存储:
- C++:
std::string、char *(C String) - Java:
String(不可变)、StringBuilder/StringBuffer(可变字符序列)
2.3.1 暴力匹配
C++
可直接使用字符串类std::string的find(str)方法进行暴力模式匹配。
时间复杂度:O(n\cdot m)
string s, p;
if (s.find(p) != -1) {
// 查找成功的操作
}
// 另一种写法
if (s.find(p) < s.size()) {
// 查找成功的操作
}Java同理
2.3.2 KMP
next数组:\text{next}[i]=以i为终点的最大公共前后缀(本文规定包含i)的长度
时间复杂度:O(n+m)
C++
char s[N], p[N]; // 主串s[1 ... n]与模式串p[1 ... m](必须从下标1开始存储字符)
int n, m; // 主串长度为n,模式串长度为m
int ne[N]; // next数组
/* 初始化 */
void init() {
scanf("%s%s", s + 1, p + 1); // 从下标1读取串至字符数组
n = strlen(s + 1), m = strlen(p + 1); // 获取有效存储长度
}
int kmp() {
/* 求模式串p的next数组:p对p自己作KMP匹配 */
for (int i = 2, j = 0; i <= m; i++) { // ne[1]=0,故i从2开始遍历
while (j && p[i] != p[j + 1]) {
j = ne[j];
}
if (p[i] == p[j + 1]) {
j++;
}
ne[i] = j; // 匹配成功则表明得到了以当前i为终点的最大公共前后缀的长度
}
/* KMP匹配 */
for (int i = 1, j = 0; i <= n; i++) { // 始终与j的下一位(j+1)作匹配
while (j && s[i] != p[j + 1]) {
j = ne[j]; // 若j未退回起点且i与j的下一位不匹配,则j回溯
}
if (s[i] == p[j + 1]) {
j++; // 若i与j的下一位匹配,则j走至下一位
}
if (j == m) { // 匹配成功的操作
return i - m;
j = ne[j]; // 若要求找到所有匹配点,则j继续回溯、匹配
}
return 0;
}
}Java
/* KMP算法模式匹配(String仍从下标0开始存储) */
public static int kmp(String str, String pattern) {
int n = str.length(), m = pattern.length();
if (m == 0) {
return 0;
}
int[] next = new int[m];
// 求pattern串的next数组
for (int i = 1, j = 0; i < m; i++) {
while (j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
if (pattern.charAt(i) == pattern.charAt(j)) {
j++;
}
next[i] = j;
}
// 字符串匹配
for (int i = 0, j = 0; i < n; i++) {
while (j > 0 && str.charAt(i) != pattern.charAt(j)) {
j = next[j - 1];
}
if (str.charAt(i) == pattern.charAt(j)) {
j++;
}
if (j == m) {
return i - m + 1;
}
}
return -1;
}2.3.3 模拟题处理思路
模拟题中字符串常见处理方式(以下均以C++为例):
2.3.3.1 截取字符串
利用s.substr()方法修缮串:
/* 截掉串头k个字符 */
s = s.substr(k);
/* 剔除下标为pos的字符 */
s = s.substr(0, pos) + s.substr(pos + 1);
/* 取倒数k个字符 */
string sf = s.substr(s.size() - k);2.3.3.2 类型转换
将字符串转换成整数、实数类的函数:
// string to int(整数)参数:字符串,起始下标(指针型,默认为0/空),字符串表示的数的进制(默认为10进制)
int stoi(const string &str, size_t *idx = 0, int base = 10)
// string to float(单精度浮点数)参数:字符串,起始下标(指针型,默认为0/空)
float stof(const string &str, size_t *idx = 0);
// string to double(双精度浮点数)参数同stof
double stod(const string &str, size_t *idx = 0);可利用如上函数来检测某数据是否属于数值类型,对非法输入会抛出错误,可用try-catch语句抓取,由此来判断是否。但这些函数返回值实为字符串前几位符合数值类型定义的部分(如stoi("6.969pog")会返回6.969而不会报错),故可创建一个下标变量idx(size_t类型)并将其地址作为第二参数传入函数,由于函数第二参数是指针型故会改变idx的值,之后比较idx与字符串长度大小来特判。
以下为用stof()判断输入字符是否为实数的代码段:
string num;
cin >> num;
float x;
bool flag = true; // 标识初始化为是
try {
size_t idx = 0;
x = stof(num, &idx);
if (idx < (int)num.size()) flag = false;
} catch (...) { // 接收错误(ERROR),这里设置为任何错误
flag = false;
}2.3.3.3 最大公共后缀
找n个串的最大公共后缀——建立串数组s[N]:
- 以
s[0]为标准串,从长到短取其长度为k的后缀(称为标准后缀):
// k为后缀长度,亦表示倒数k个字符
string sf = s[0].substr(s[0].size() - k);- 每轮的标准后缀依次与剩余
n - 1个串比较,判断不匹配条件:
// 标准后缀长度k大于某串或发生不匹配
if (k > s[i].size() || s[i].substr(s[i].size() - k) != sf) ...- 发生不匹配则立即结束此轮后缀比较,执行下一轮;跳出比较循环则表示找到最大公共后缀。
2.3.3.4 数字串拼接最小数
求一组数字串能拼接成的最小数,使用std::sort()时可定义如下排序函数排列串:
bool cmp(string a, string b) {
return a + b < b + a;
}2.3.3.5 格式化输入输出
使用函数sscanf(...)可格式化读入字符串中的有用数据(配合上一条即可按字符串特征编写相对应的算法读入所需数据)。与之对应的函数sprintf(...)可格式化赋回字符串,效果类似直接相加。
两种结果输出方式:
- 现场输出(无重度修改需求)
- 用
std::string串res存储结果,最终修缮后统一输出(对格式要求高,如对行末空格的处理)
对于需要将字符按特定图形输出的,除了即时输出外,还可选择开一个矩阵,将字符填入,最后遍历矩阵输出(尽量分治)。
2.3.3.6 时空差的计算
时空差计算方式:
- 定基准:以某点
\{0\}为原点,统一单位,将\{b\}\ - \{a\}转化为(\{b\} - \{0\}) - (\{a\} - \{0\}) - 以空间换时间:推广前缀和算法的思想,提前算出定义域上各时间点$i$上的值(
\{i\} - \{0\}),可用递推将结果存入容器中。- 例:求某秒在当天对应时刻距离原点累积收费:
for (int i = 1; i < MAXD; ++i)
sum[i] = sum[i - 1] + cost[(i - 1/*1*/) % 1440/*2*/ / 60/*3*/];
// 注:
// 1(i - 1):题中规定收费区间左闭右开
// 2(取余于1440):定位至一天内
// 3(除以60):换算成小时(会自动取整)- 提前剪枝:如银行多窗口排队问题,窗口结束服务时刻早于下一个来访者(期间保持空闲),则可直接将结束服务时刻挪至来访者到来时刻,便于后续计算(省去判别异常情况)。
2.3.3.7 对象存储
高效存储对象数据:可用map或unordered_map将对象与其结构体一一对应,或者押入vector或堆中。
自定义结构体排序——重载不等号:数组重载小于号(<),优先队列重载大于号(>)(同std::sort()中cmp函数。记忆:数组左观,优先队列右观)。
语法(以小于号为例,将学生结构体按人名字典序比较):
bool operator<(const Student& t) const {
return name < t.name;
}2.4 Trie树
字典树(Retrieval Tree, Trie Tree)用于高效存储和查找字符串集合。
AC自动机为追加了fail指针的Trie树,算法思想参考KMP。
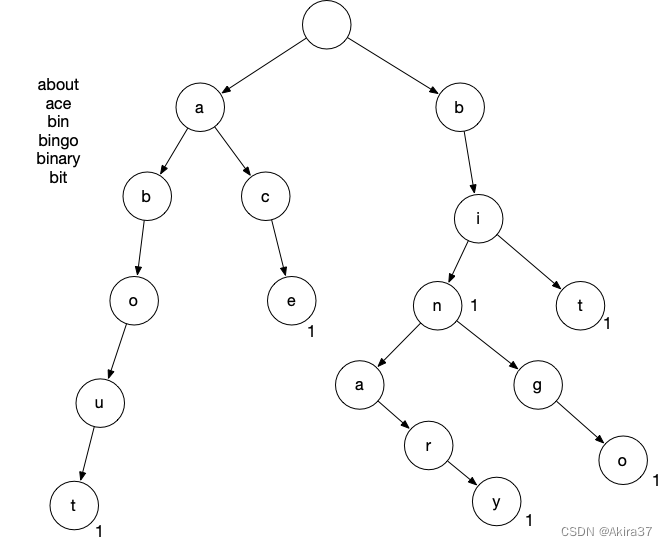
C++
int son[N][26], cnt[N], idx;
// son[p][u]记录结点p的第u个子结点(26表示26个字母)
// cnt[p]存储以结点p结尾的单词数量
// idx初始为0(0号点既是根结点,又是空结点,故创建结点时为++idx)
/* 插入一个字符串 */
void insert(char str[]) {
int p = 0; // 从根结点0开始遍历Trie的指针
for (int i = 0; str[i]; i++) {
int u = str[i] - 'a';
if (!son[p][u]) {
son[p][u] = ++idx; // 不存在则创建该子结点
}
p = son[p][u];
}
cnt[p]++; // p最终指向字符串末尾字母,p计数器自增
}
/* 查询字符串出现的次数 */
int query(char str[]) {
int p = 0;
for (int i = 0; str[i]; i++) {
int u = str[i] - 'a';
if (!son[p][u]) {
return 0; // 不存在则直接返回0
}
p = son[p][u];
}
return cnt[p]; // p最终指向字符串末尾字母,返回数量
}Java
static int[][] son = new int[N][26]; // son[p][u]记录结点p的第u个子结点
static int[] cnt = new int[N]; // cnt[p]存储以结点p结尾的单词数量
static int idx = 0; // idx初始为0(0号点既是根结点,又是空结点)
/* 插入一个字符串 */
public static void insert(String str) {
int p = 0; // 从根结点0起遍历Trie的指针
for (int i = 0; i < str.length(); i++) {
int u = str.charAt(i) - 'a'; // 将字符转换为对应的索引
if (son[p][u] == 0) {
son[p][u] = ++idx; // 不存在则创建该子结点
}
p = son[p][u]; // 更新指针走向当前子结点
}
cnt[p]++; // p最终指向字符串末尾字母,p计数器自增
}
/* 查询字符串出现的次数 */
public static int query(String str) {
int p = 0; // 从根结点开始
for (int i = 0; i < str.length(); i++) {
int u = str.charAt(i) - 'a'; // 将字符转换为对应的索引
if (son[p][u] == 0) {
return 0; // 不存在则直接返回0
}
p = son[p][u]; // 更新指针至下一个结点
}
return cnt[p]; // p最终指向字符串末尾字母,返回数量
}2.5 并查集
使用树的双亲表示法顺序存储(下标从1开始),p[x]存储结点x的父结点(经过路径更新后变为该结点所属集合的根结点/祖宗结点)。若p[x] == x(或find(x) == x),则x为该集合的根结点。
判断结点a和b是否在同一集合:find(a) == find(b)
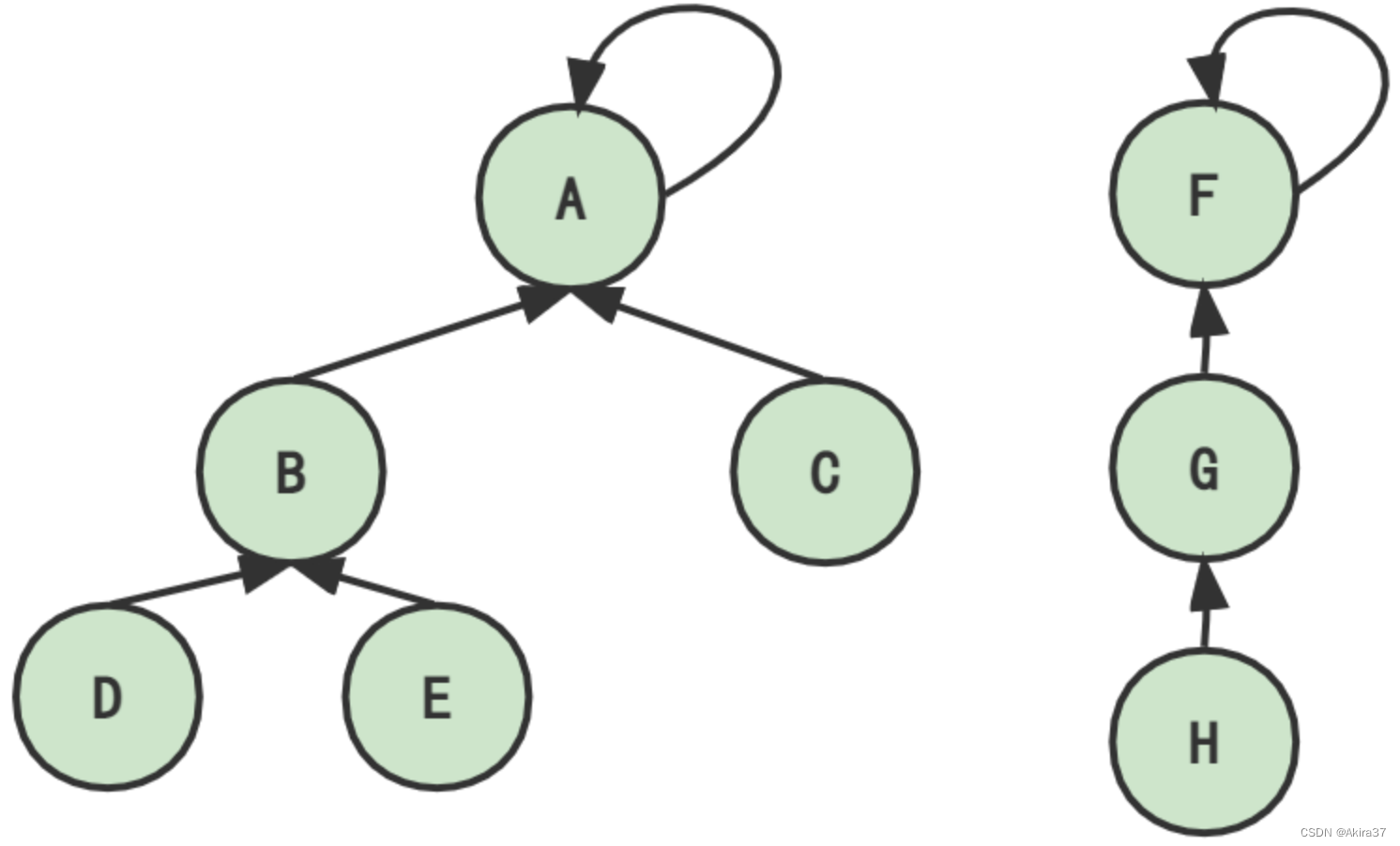
2.5.1 朴素并查集
C++
int n; // [1 ... n]
int p[N]; // p[i]存储结点i的祖先结点(路径压缩后则为根结点),集合根结点的父结点为其自身
/* 初始化 */
void init() {
for (int i = 1; i <= n; i++) {
p[i] = i;
}
}
/* 并查集核心操作:返回结点x所属集合的根结点,并进行路径压缩 */
int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
/* 合并结点a和b所在集合:将a并至b */
void Union(int a, int b) {
p[find(a)] = find(b); // 将a的根接在b的根之后
}Java
static int n;
static int[] p; // p[1 ... n],p[i]存储结点i的祖先(路径压缩后则为根结点)
/* 初始化 */
public static void init() {
for (int i = 1; i <= n; i++) {
p[i] = i;
}
}
/* 并查集核心操作:返回结点x所属集合的根结点,并进行路径压缩 */
public static int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
/* 合并结点a和b所在集合:将a并至b */
public static void union(int a, int b) {
p[find(a)] = find(b); // 将a的根接在b的根之后
}2.5.2 维护集合大小的并查集
结点a所属集合的大小:cnt[find(a)]
C++
int n;
int p[N], cnt[N]; // cnt[i]存储根结点i的集合中结点数(仅根结点的cnt有意义)
/* 初始化 */
void init() {
for (int i = 1; i <= n; i++) {
p[i] = i;
cnt[i] = 1; // 初始化各结点为根,其所属集合大小为1
}
}
/* 并查集核心操作(同前述) */
int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
/* 合并结点a和b所在集合:将a并至b */
void Union(int a, int b) {
if (find(a) == find(b)) continue; // 若已在同一集合内则跳过
cnt[find(b)] += cnt[find(a)]; // 需将a所属集合的大小加至b
p[find(a)] = find(b);
}Java
static int n;
static int[] p;
static int[] cnt; // cnt[i]存储根结点i的集合中结点数(仅根结点的cnt有意义)
/* 初始化 */
public static void init() {
for (int i = 1; i <= n; i++) {
p[i] = i;
cnt[i] = 1; // 初始化各结点为根,其所属集合大小为1
}
}
/* 并查集核心操作(同前述) */
public static int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
/* 合并结点a和b所在集合:将a并至b */
public static void union(int a, int b) {
if (find(a) == find(b)) return; // 若已在同一集合内则跳过
cnt[find(b)] += cnt[find(a)]; // 需将a所属集合的大小加至b
p[find(a)] = find(b);
}
2.5.3 维护到祖宗结点距离的并查集
C++
int n;
int p[N], d[N]; // d[i]存储结点i到其根结点p[i]的距离
/* 初始化 */
void init() {
for (int i = 1; i <= n; i++) {
p[i] = i;
d[i] = 0; // 初始化全为0
}
}
/* 并查集核心操作 */
int find(int x) {
if (p[x] != x) {
int u = find(p[x]); // u临时记录根结点
d[x] += d[p[x]]; // 更新x到根p[x]的路径长度
p[x] = u;
}
return p[x];
}
/* 根据具体问题,初始化根find(a)的偏移量 */
void set_distance(int a, int distance) {
d[find(a)] = distance;
}
/* 合并结点a和b所在集合:将a并至b(同前述) */
void Union(int a, int b) {
p[find(a)] = find(b);
}Java
static int n;
static int[] p;
static int[] d; // d[i]存储结点i到其根结点p[i]的距离
/* 初始化 */
public static void init() {
for (int i = 1; i <= n; i++) {
p[i] = i;
d[i] = 0; // 初始化全为0
}
}
/* 并查集核心操作 */
public static int find(int x) {
if (p[x] != x) {
int u = find(p[x]); // u临时记录根结点
d[x] += d[p[x]]; // 更新x到根p[x]的路径长度
p[x] = u;
}
return p[x];
}
/* 根据具体问题,初始化根find(a)的偏移量 */
public static void setDistance(int a, int distance) {
d[find(a)] = distance;
}
/* 合并结点a和b所在集合:将a并至b(同前述) */
public static void union(int a, int b) {
p[find(a)] = find(b);
}2.6 堆
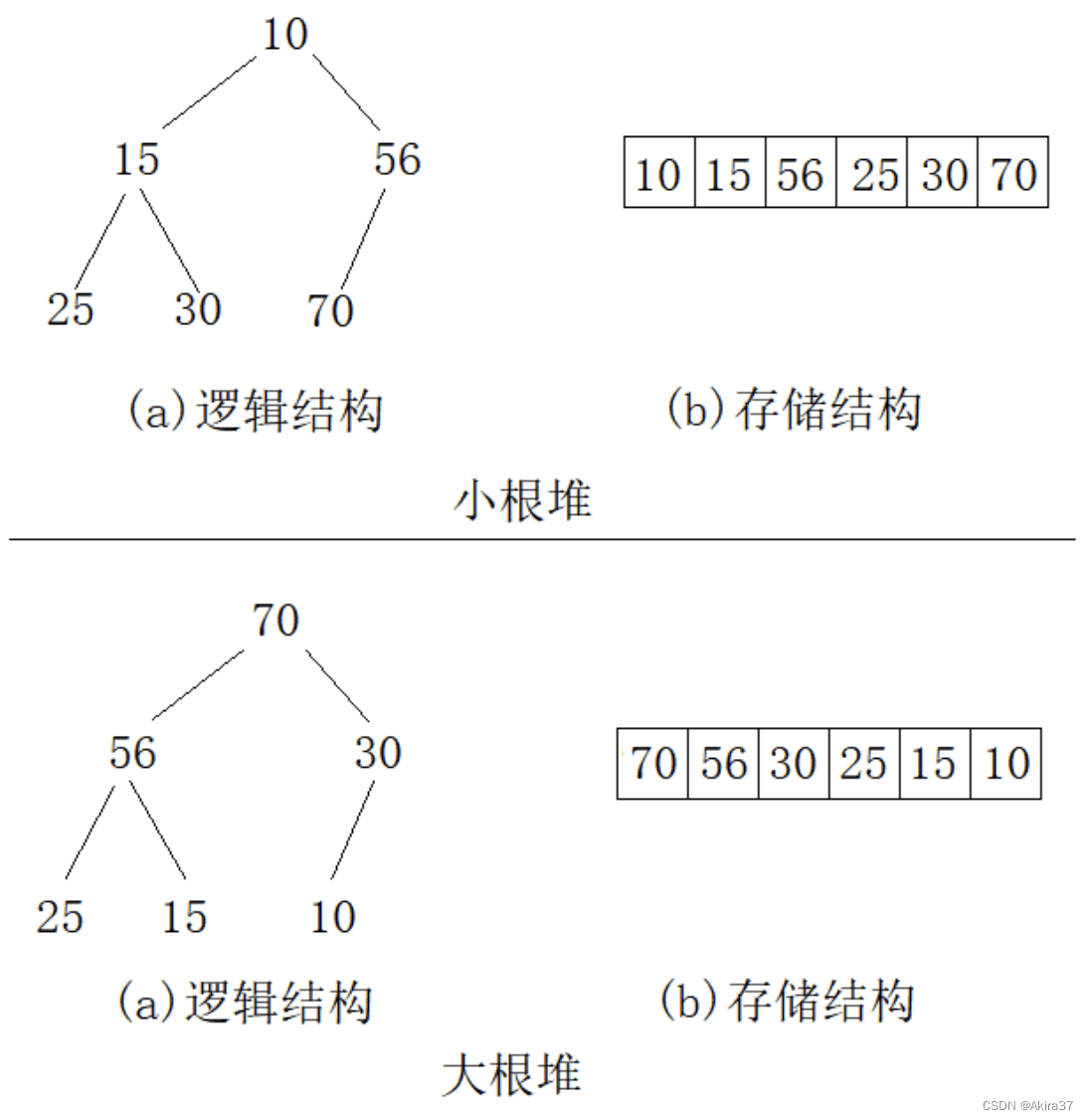
2.6.1 朴素堆
C++
可直接使用std::priority_queue<int>快速实现,默认为大根堆,可自定义比较规则以实现小根堆(更常用),高效查找最小值:
priority_queue<int> max_heap; // 默认为大根堆
priority_queue<int, vector<int>, greater<int> > min_heap; // 小根堆或使用数组建堆(此处以小根堆为例),注意元素存储范围为[1, n]:
int h[N], n;
// h[1 ... n]为小根堆,h[1]为堆顶/最小值,结点u的双亲为u/2,左右孩子分别为2*u、2*u+1(若存在)
/* 向下调整:一路向下交换结点u与其较小的儿子 */
void down(int u) {
int t = u; // 记录u、2u、2u+1三个结点中的最小值结点编号
if (u * 2 <= n && h[u * 2] < h[t]) {
t = u * 2;
}
if (u * 2 + 1 <= n && h[u * 2 + 1] < h[t]) {
t = u * 2 + 1;
}
if (u != t) {
swap(u, t);
down(t);
}
}
/* 向上调整 */
void up(int u) {
while (u / 2 && h[u] < h[u / 2]) {
swap(u, u / 2);
u /= 2;
}
}
/* O(n)建堆 */
for (int i = n / 2; i; i--) {
down(i);
}Java
同理,可使用内置的PriorityQueue,但默认为小根堆(与C++中相反),可通过初始化时传入Comparator参数实现大根堆,Lambda表达式为(a, b) -> b - a:
Queue<Integer> minHeap = new PriorityQueue<>(); // 小根堆
Queue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a); // 大根堆2.6.2 维护映射关系的堆
可实现堆中任意元素的插入删除操作,并建立与原始插入序列之间的映射关系(以下以小根堆为例):
C++
int h[N], cnt;
int ph[N], hp[N], idx;
// h[1 ... cnt]为小根堆:h[1]为堆顶/最小值,结点u的双亲为u/2,左右孩子分别为2*u、2*u+1(若存在)
// ph[k]映射插入序列中第k个点到堆中的下标u (Position-Heap)
// hp[u]映射堆中结点u到插入序列中的序号k (Heap-Position)
/* 堆swap函数:交换堆中两个结点a和b的所有信息(若不建立映射则用std::swap()即可) */
void heap_swap(int a, int b) {
swap(ph[hp[a]], ph[hp[b]]);
swap(hp[a], hp[b]);
swap(h[a], h[b]);
}
/* 向下调整:一路向下交换结点u与其较小的儿子 */
void down(int u) {
int t = u; // 记录u、2u、2u+1三个结点中的最小值结点编号
if (2 * u <= cnt && h[2 * u] < h[t]) {
t = 2 * u;
}
if (2 * u + 1 <= cnt && h[2 * u + 1] < h[t]) {
t = 2 * u + 1;
}
if (t != u) {
heap_swap(u, t);
down(t);
}
}
/* 向上调整:一路向上交换结点u与其父结点 */
void up(int u) {
while (u / 2 && h[u / 2] > h[u]) {
heap_swap(u / 2, u);
u >>= 1;
}
}
/* 插入一个数x */
void insert(int x) {
cnt++, idx++;
ph[idx] = cnt;
hp[cnt] = idx;
h[cnt] = x;
up(cnt);
}
/* 删除最小值/堆顶元素 */
void remove_top() {
heap_swap(1, cnt);
cnt--;
down(1);
}
/* 删除第k个插入的元素 */
void remove(int k) {
int u = ph[k];
heap_swap(u, cnt);
cnt--;
up(u); // 只会执行其中一个
down(u);
}
/* 修改第k个插入的元素为x */
void change(int k, int x) {
int u = ph[k];
h[u] = x;
up(u); // 只会执行其中一个
down(u);
}2.7 哈希
内置哈希表容器:
- C++:
std::unordered_set、std::unordered_map。 - Java:
HashSet、HashMap。
当使用数组实现时,对于一般哈希,N尽量取质数,使得冲突概率尽可能低。
若要删除,可额外开bool数组st[]标记各地址元素状态来表示是否被删(同前述)。
2.7.1 拉链法
C++
int h[N], e[N], ne[N], idx;
/* 链表初始化 */
void init() {
memset(h, -1, sizeof h);
}
/* 向哈希表中插入一个数 */
void insert(int x) {
int t = (x % N + N) % N; // C++的负数取余运算:(-n) mod k = -(n mod k)
e[idx] = x;
ne[idx] = h[t];
h[t] = idx++; // 将x头插在链表h[t]
}
/* 在哈希表中查询某个数是否存在 */
bool find(int x) {
int t = (x % N + N) % N;
for (int i = h[t]; ~i; i = ne[i]) { // 遍历整条链表h[t]
if (e[i] == x) {
return true;
}
}
return false;
}2.7.2 开放寻址法
数组长度应开到最大数据量的2~3倍。
C++
const int INF = 0x3f3f3f3f; // 表示该哈希值的元素不在哈希表内
int h[N];
/* 哈希表初始化 */
void init() {
memset(h, 0x3f, sizeof h); // 初始化为无穷
}
/* 若x在哈希表中,返回x的下标;否则返回x应该插入的位置*/
int find(int x) {
int t = (x % N + N) % N;
while (h[t] != INF && h[t] != x) { // 若已存在该哈希值的元素且该元素不等于x
t++;
if (t == N) t = 0;
}
return t;
}2.7.3 字符串哈希
字符串前缀哈希法:快速判断两段字符串是否相等(不考虑冲突)
- 核心思想:将字符串看成
P进制数,P的经验值为131或13331,取这两个值的冲突概率极低 - C++小技巧:取模的数用
2^{64},这样直接用unsigned long long存储,溢出的结果就是取模的结果
C++
typedef unsigned long long ULL;
const int P = 131;
char str[N]; // 待哈希字符串str[1 ... n]
int n; // 字符串的长度
ULL h[N], p[N]; // h[k]存储字符串前k个字母的哈希值(前缀和),p[k]存储 P^k mod 2^64
/* 预处理前缀哈希 */
void init() {
p[0] = 1;
for (int i = 1; i <= n; i++) {
h[i] = h[i - 1] * P + str[i]; // 求前缀和
p[i] = p[i - 1] * P; // unsigned long long溢出相当于对2^64取模
}
}
/* 计算子串str[l ... r]的哈希值 */
ULL get(int l, int r) {
return h[r] - h[l - 1] * p[r - l + 1];
}2.8 对顶堆
C++实现:使用两个multiset(std::multiset),上大下小。上下堆的大小差应时刻保持不超过1。
应用:快速查询有序序列的中位数,中位数从属于哪个堆与元素数为偶数(n=2k)时取孰为中位有关:
- 通常取中位为
\frac {n}2,则中位处于较小的下堆。此时下堆大小可以比上堆多1。 - 取
\frac n2+1时,各种情形与上述相反
3 搜索与图论
邻接矩阵与邻接表、DFS、BFS、拓扑排序、最短路径、最小生成树、二分图
3.1 图的存储方式
一般的树均可用图的方式来存储,无向图相当于弧均双向的特殊的有向图。
3.1.1 邻接矩阵
注意无法存储重边,因此通常选择存储所有重边权中的最值。适合存稠密图,可随机存取任意边。
C++
int g[N][N]; // g[a][b]存储有向边<a, b>
/* 初始化 */
void init() {
memset(g, 0x3f, sizeof g);
}
/* 获取边<a, b> */
int get(int a, int b) {
return g[a][b];
}3.1.2 邻接表
相当于同时开n条无头单链表,表h[k]存储点k的所有出边。适合存稀疏图,可快速遍历某点的所有出边。
C++
n叉静态链表写法:
const int N = 1e5, M = 2 * N;
int n, m; // 点数、边数
int h[N], e[M], ne[M], idx; // h[k]为点k的边表的头指针
/* 初始化 */
void init() {
memset(h, -1, sizeof h);
idx = 0;
}
/* 添加一条边<a, b> */
void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}二维vector写法:
// 二维容器内存放一维容器下标所指向的结点
vector<vector<int> > g;
vector<int> g[N]; // (等价写法)有时还需存储边的权值(点到点的距离),可额外定义一个有序数对类型存储:
typedef pair<int, int> PII;
// 有序数对PII(Pair of Integer-Integer)
// first:结点编号,second:距离
vector<vector<PII> > g;
vector<PII> g[N]; // (等价写法)3.1.3 边的结构体
很多情景(如顶点覆盖问题)着重考察边(及其两个端点)的性质(如连通性),这些性质通常与多点宏观关系(如路径)无关,并且该情况下常采用顶点对的形式读入数据,因此适合使用简单结构体数组存储。这种数据结构的空间利用率高于邻接矩阵,相对于邻接表更方便直接遍历所有边。有时需要操作大量集合时也常与并查集结合使用:
C++
struct edge {
int a, b; // 边的两个顶点(默认为有向边<a, b>)
int w; // 边的权
} e[N];3.2 搜索算法
DFS与BFS的时间复杂度均为O(n+m)
3.2.1 深度优先搜索(DFS)
DFS技巧:
- 分析问题:画图、归纳
- 保存现场
- 剪枝
- 偏移量:适用于各种DFS、BFS等矩阵遍历情形。控制点在二维平面上移动的方向(搜索方向),可设定方向下标按顺时针(上、右、下、左)递增。此时对于方向下标
i,其反方向下标为i ^ 2(对2做按位异或运算),亦可手动if设置求得。// 上(-1, 0),右(0, 1),下(1, 0),左(0, -1) int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
示例:
C++
bool st[N];
int dfs(int u) {
st[u] = true;
for (int i = h[u]; ~i; i = ne[i]) { // 遍历u的所有出边
int v = e[i];
if (!st[v]) {
dfs(v);
}
}
}3.2.2 宽度优先搜索(BFS)
BFS技巧:
- 必要时开距离数组记录第一次到达每个点时的距离(即为到达每个点的最短路距离)
- 求多源最短路时,可以设立一个超级源点(指向各源点的出边权值为0),则将问题转化为从超级源点到终点的单源最短路径。实际用BFS求时只需在初始化时将所有源点一次性入队即可。
示例:
C++
bool st[N]; // V: [1 ... n]
void bfs() {
queue<int> q;
q.push(1); // 队中压入源点
st[1] = true;
while (!q.empty()) {
int t = q.front();
q.pop();
for (int i = h[t]; ~i; i = ne[i]) { // 遍历点t的所有出边
int u = e[i];
if (!st[u]) {
st[u] = true;
q.push(u);
}
}
}
}3.2.3 检测图的连通性
连通图条件:生成树的边数为顶点数(dfs(1) == n)。
使用DFS/BFS判别(以DFS为例):
C++
int n;
bool g[N][N], st[N];
/* DFS检测连通性 */
int dfs(int u) {
st[u] = true;
/* 可额外添加“输出”、“入vector”、“计入权值”等操作,以下递归入口前后同理 */
int res = 1; // 可走到的顶点数
for (int i = 1; i <= n; ++i)
if (!st[i] && g[u][i])
res += dfs(i);
return res;
}
/* 连通图条件:生成树的边数为顶点数 dfs(1) == n */使用并查集计算图中的连通块数量(建议使用边的结构体存储各边):
- 法一:用变量
cnt记录当前连通块的数量(初始化为顶点数,有时根据题意会事先剔除k个顶点则再减k),遍历边数组,使用并查集合并每条边的两个端点(若符合题意),每合并一条就将cnt自减1。最后cnt即为所求结果,cnt - 1即为恢复成连通图需要添加的最少边数。 - 法二:合并顶点操作同法一,但不实时记录连通块数量,合并结束后从头遍历并查集,其中的祖宗结点个数即为结果(与上同理,如有特殊要求则需减去剔除的顶点数)。
3.3 二叉树
关于树与二叉树的理论知识请参阅《数据结构强化笔记》。
3.3.1 二叉树的存储方式
二叉树最常用二叉链表存储结构存储,亦可使用各种顺序存储结构,可按实际需求灵活挑选使用:
C++
int l[N], r[N], idx;
// 二叉链表存储结构:l[k]、r[k]分别存储结点k的左右孩子
// idx初始为0,指向下一个结点可用地址
int tr[N];
// 孩子表示法:tr[k]存储结点k的孩子。通常会造成大量空间浪费(空分枝对应的元素不赋值),故仅适合存储完全二叉树(CBT)
// 从下标1开始存储完全二叉树,结点u的双亲为u/2,左右孩子分别为2*u、2*u+1(若存在)
// 格外适合堆的存储,详见前述
int p[N];
// 双亲表示法:p[k]存储结点k的双亲。适合着重考察父子关系的场景(如树形DP或求最近公共祖先(LCA)时)3.3.2 二叉树的确定
常需利用先序和中序或后序和中序遍历序列建立二叉树。使用先序和后序遍历序列无法唯一确定二叉树,对此一般要求不高(暴力枚举左右子树范围即可得至少一棵树),故以下只探讨前两种情况:
- 读入序列时可提前用
std::unordered_map映射各结点在中序序列中的位置pos,便于建树时快速定位子树根root的中序下标pos[root],节省大量查找时间。 - 关于递归入口的区间范围:除去既定结点,保证两段待定区间长度相等即可。伪代码示例如下(无需死记,只需利用各遍历序列基本特性,确保区间长度相等即可):
C++
// 建树函数伪代码
typename build(int in_l, int in_r, int pre_l | post_l, int pre_r | post_r) {
/* 例1:先序中序建树 */
int root = pre[pre_l];
int k = pos[root];
// ...
lchild : build(in_l, k - 1, pre_l + 1, pre_l + 1 + (k - 1 - in_l))
rchild : build(k + 1, in_r, preL + 1 + (k - 1 - in_l) + 1, pre_r)
// ...
/* 例2:后序中序建树 */
int root = post[post_r];
int k = pos[root];
// ...
lchild : build(in_l, k - 1, post_l, post_l + (k - 1 - in_l))
rchild : build(k + 1, in_r, post_l + (k - 1 - in_l) + 1, post_r - 1)
// ...
}- 建树的实质依旧是DFS,故有时并不一定要存储树,可在递归入口前后直接执行各种要求操作,少走弯路。
- 利用中序和层次遍历序列同样可以确定一棵二叉树,但考察极少,暂时不作阐述。
3.3.3 二叉排序树(BST)
定义:每个结点的权值大于左子树且小于右子树的二叉树。
特点:中序遍历序列递增有序。将无序的前序/后序遍历序列排序即得中序,故只根据前序/后序任一遍历序列即可建BST。
3.3.4 平衡二叉树(AVL树)
定义:所有结点的左右子树高度差(平衡因子,Balance Factor)的绝对值|BF|≤1的二叉排序树称为平衡二叉树(AVL树)
平衡因子计算式:BF = h(左子树) - h(右子树)
以下分别为AVL树的数据结构、获取属性、旋转调整操作、插入操作(对于AVL树只需掌握插入,对删除不作要求)的代码实现:
C++
int l[N], r[N], v[N], h[N], idx;
// v[]:结点权值
// h[]:结点高度
/* 更新子树根高度 */
void update(int u) {
h[u] = max(h[l[u]], h[r[u]]) + 1;
}
/* 计算子树根的平衡因子 */
int get_bf(int u) {
return h[l[u]] - h[r[u]];
}
/* 左旋子树根 */
void L(int &u) {
int p = r[u];
r[u] = l[p], l[p] = u;
update(u), update(p);
u = p;
}
/* 右旋子树根 */
void R(int &u) {
int p = l[u];
l[u] = r[p], r[p] = u;
update(u), update(p);
u = p;
}
/* 在子树根u处插入权值w的结点 */
void insert(int &u, int w) {
if (!u) { // 插入
u = ++idx;
v[u] = w;
} else if (w < v[u]) {
insert(l[u], w);
if (getBF(u) == 2) { // L
if (getBF(l[u]) == 1) { // LL型,右单旋
R(u);
} else { // LR型,先左旋再右旋
L(l[u]);
R(u);
}
}
} else { /* 此处保证输入流中无重复权值 */
insert(r[u], w);
if (getBF(u) == -2) { // R
if (getBF(r[u]) == -1) { // RR型,左单旋
L(u);
} else { // RL型,先右旋再左旋
R(r[u]);
L(u);
}
}
}
update(u);
}3.4 最短路径
原理解析详见《数据结构强化笔记》。
3.4.1 朴素Dijkstra算法
时间复杂度:O(n^2+m)
适用情形:稠密图
C++
int n; // V: [1 ... n]
int g[N][N]; // 邻接矩阵图(带权)
int dist[N]; // dist[]存储起点到每个点的最短路径
bool st[N]; // st[]标记每个点的最短路是否已被确定
/* 求起点S到终点T的最短路,若不存在则返回-1 */
int dijkstra(int S, int T) {
memset(dist, 0x3f, sizeof dist);
dist[S] = 0; // 这里只先设起点的dist
for (int i = 0; i < n; i++) { // 迭代n次(第1轮预处理起点)
int t = -1; // 在还未确定最短路的点中,寻找最短距离点t
for (int j = 1; j <= n; j++) {
if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
}
st[t] = true;
for (int j = 1; j <= n; j++) { // 用t更新其他点的距离
if (dist[j] > dist[t] + g[t][j]) {
dist[j] = dist[t] + g[t][j];
}
}
}
if (dist[T] == 0x3f3f3f3f) return -1;
return dist[T];
}3.4.2 堆优化Dijkstra算法
时间复杂度:O(m\log n)
适用情形:稀疏图
C++
typedef pair<int, int> PII;
int n; // V: [1 ... n]
int h[N], e[M], w[M], ne[M], idx; // 邻接表图,w[i]存边i的权值
int dist[N]; // dist[]存储起点到每个点的最短路径
bool st[N]; // st[]标记每个点的最短路是否已被确定
/* 求起点S到终点T的最短路,若不存在则返回-1 */
int dijkstra(int S, int T) {
memset(dist, 0x3f, sizeof dist);
dist[S] = 0; // 这里也只先设起点的dist
priority_queue<PII, vector<PII>, greater<PII> > heap; // 小根堆
heap.push({0, S}); // (distance, vertex)
while (!heap.empty()) {
auto t = heap.top();
heap.pop();
int u = t.second, distance = t.first; // 用堆得到最近的点及与其距离
if (st[u]) continue; // 若已确定则跳过
st[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (dist[v] > distance + w[i]) {
dist[v] = distance + w[i];
heap.push({dist[v], v});
}
}
}
if (dist[T] == 0x3f3f3f3f) return -1;
return dist[T];
}3.4.3 Bellman-Ford算法
时间复杂度:O(nm)
适用情形:存在负权边的图
C++
int n, m; // V: [1 ... n]
struct Edge {
int a, b, w;
} edges[M]; // 边集,存储权值为w的有向边<a, b>
int dist[N]; // dist[]存储起点到每个点的最短路径
/* 求起点S到终点T的最短路,若不存在则返回-1 */
int bellman_ford(int S, int T) {
memset(dist, 0x3f, sizeof dist);
dist[S] = 0;
for (int i = 0; i < n; i++) { // 要求最大长度为n的最短路径,故迭代n次
for (int j = 0; j < m; j++) { // 每次遍历全部m条边
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > dist[a] + w) { // 松弛操作:更新当前dist
dist[b] = dist[a] + w;
}
}
}
if (dist[T] > 0x3f3f3f3f / 2) return 0x3f3f3f3f; // 因为负权边的存在,可能略低于INF
return dist[T];
}应用:求有边数限制的最短路
限制k条边就进行k轮迭代遍历,遍历开始前需先备份 dist[]于 backup[],用其将 dist[]更新。
C++
int n, m, k; // 限制最短路最多经过k条边
struct Edge {
int a, b, w;
} edges[M];
int dist[N], backup[N]; // backup[]备份dist[]数组,防止发生串联(用改后数据去改别人)
/* 求起点S到终点T的最短路,若不存在则返回-1 */
int bellman_ford(int S, int T) {
memset(dist, 0x3f, sizeof dist);
dist[S] = 0;
for (int i = 0; i < k; i++) { // 限制k条边,则迭代k次
memcpy(backup, dist, sizeof dist); // 遍历边前先将dist拷贝至备份数组
for (int j = 0; j < m; j++) {
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
if (dist[b] > backup[a] + w) { // 使用备份数组做松弛操作
dist[b] = backup[a] + w;
}
}
}
if (dist[T] > 0x3f3f3f3f / 2) return 0x3f3f3f3f;
return dist[T];
}3.4.4 SPFA算法
时间复杂度:平均O(m),最坏O(nm)
队列优化的Bellman-Ford算法,后继变小了当前dist才变小。
C++
int n; // V: [1 ... n]
int h[N], e[M], w[M], ne[M], idx; // 邻接表图,w[i]存边i的权值
int dist[N]; // dist[]存储起点到每个点的最短路径
bool st[N]; // st[]标记每个点的最短路是否已被确定
int spfa(int S, int T) {
memset(dist, 0x3f, sizeof dist);
dist[S] = 0;
queue<int> q; // 队中存放待更新的点(用堆也行)
q.push(S);
st[S] = true; // 结点入队时做标记
while (!q.empty()) { // 使用BFS的思想
auto t = q.front();
q.pop();
st[t] = false; // 结点出队时撤销标记(之后可能需再次入队被更新)
for (int i = h[t]; ~i; i = ne[i]) {
int u = e[i];
if (dist[u] > dist[t] + w[i]) {
dist[u] = dist[t] + w[i];
if (!st[u]) { // 若更新了u的距离,则其出边所指也可能待更新,判断将其入队
q.push(u);
st[u] = true;
}
}
}
}
if (dist[T] == 0x3f3f3f3f) return 0x3f3f3f3f;
return dist[T];
}应用:判断图中是否存在负环
时间复杂度:O(nm)
不需要初始化 dist[],因此之后正权入边顶点永不会被更新。并且为了消除某点可能无法到达负环的影响,将所有点全入队并标记!
原理:若某条最短路径上有n个点(除了自己),则加上自己之后一共有n+1个点,由抽屉原理一定有两个点相同,故存在负环。
C++
int n;
int h[N], e[M], w[M], ne[M], idx;]
int dist[N], cnt[N]; // cnt[x]存储起点(任意)到x的最短路中经过的点数
bool st[N];
/* 如果存在负环,则返回true,否则返回false */
bool spfa() {
queue<int> q; // 不需要初始化dist数组,直接将所有点全入队并标记!
for (int i = 1; i <= n; i++) {
q.push(i);
st[i] = true;
}
while (!q.empty()) {
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; ~i; i = ne[i]) {
int u = e[i];
if (dist[u] > dist[t] + w[i]) {
dist[u] = dist[t] + w[i];
cnt[u] = cnt[t] + 1; // 若更新了u的距离,则立即更新其cnt(前驱加1)
if (cnt[u] >= n) return true; // 若最短路已包含至少n个点(不含自身),则有负环
if (!st[u]) {
q.push(u);
st[u] = true;
}
}
}
}
return false; // 跳出循环则说明无负环
}3.4.5 Floyd算法
时间复杂度:O(n^3)
基于动态规划
C++
int n, m; // V: [1 ... n]
int dist[N][N]; // 邻接矩阵图,经过Floyd()操作后变为存储最短距离
/* 初始化 */
void init() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j) {
dist[i][j] = 0;
} else {
dist[i][j] = 0x3f3f3f3f; // 之后被更新为边权
}
}
}
}
/* 算法结束后,d[a][b]表示a到b的最短距离 */
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}3.5 最小生成树
原理解析详见《数据结构强化笔记》。
3.5.1 朴素版Prim算法
时间复杂度:O(n^2+m)
必须先累加 res再更新 dist[],以避免负自环污染当前 t最短距离
C++
const int INF = 0x3f3f3f3f;
int n; // V: [1 ... n]
int g[N][N]; // 邻接矩阵图
int dist[N]; // dist[]存储起点到当前最小生成树(MST)的最短距离
bool st[N]; // st[]标记每个点是否已经在生成树中
/* 若图不连通,则返回INF,否则返回最小生成树的最小代价 */
int prim() {
memset(dist, 0x3f, sizeof dist); // 仅计算最小代价,故无需另设起点,不应先置标记为true
int res = 0; // 存储最小代价
for (int i = 0; i < n; i++) { // 迭代n次(第1轮预处理生成树根)
int t = -1; // 在还未并入MST的点中,寻找最短距离点t
for (int j = 1; j <= n; j++) {
if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
}
if (i && dist[t] == 0x3f3f3f3f) return 0x3f3f3f3f; // 从第2轮起,若最短距离为无穷,则说明不连通
if (i) {
res += dist[t]; // 从第2轮起,将t的距离计入最小代价(须先累加res)
}
st[t] = true; // 将t并入MST
for (int j = 1; j <= n; j++) { // 用新并入的t更新各点到生成树的距离
if (dist[j] > g[t][j]) { // 与dij不同,不应加前驱的dist(求取到整棵树的距离)
dist[j] = g[t][j];
}
}
}
return res;
}3.5.2 Kruskal算法
时间复杂度:O(m\log m)
C++
int n, m; // V: [1 ... n]
struct Edge {
int a, b, w;
bool operator<(const Edge &t) const { // 重载运算符,用于按权递增排序
return w < t.w;
}
} edges[MAXM]; // 边集,存储权值为w的有向边<a, b>
int p[N]; // 并查集
/* 并查集核心操作 */
int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
/* 若图不连通,则返回INF,否则返回最小生成树的最小代价 */
int kruskal() {
sort(edges, edges + m); // 将边按权递增排序(方式不限)
for (int i = 1; i <= n; i++) {
p[i] = i;
}
int res = 0, cnt = 0;
for (int i = 0; i < m; i++) { // 枚举所有边,将合适的边并入MST(加入集合)
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
if (find(a) != find(b)) { // 如果两个连通块不连通,则将这两个连通块合并
p[find(a)] = find(b);
res += w;
cnt++;
}
}
if (cnt < n - 1) return 0x3f3f3f3f; // 判定连通性(连通的必要条件:|E| = |V| - 1)
return res;
}3.6 二分图
定义:二分图可将图中顶点划分两个集合,使得集合内顶点互不邻接,不同集合顶点可邻接
定理:图为二分图\Leftrightarrow图中不含奇数环
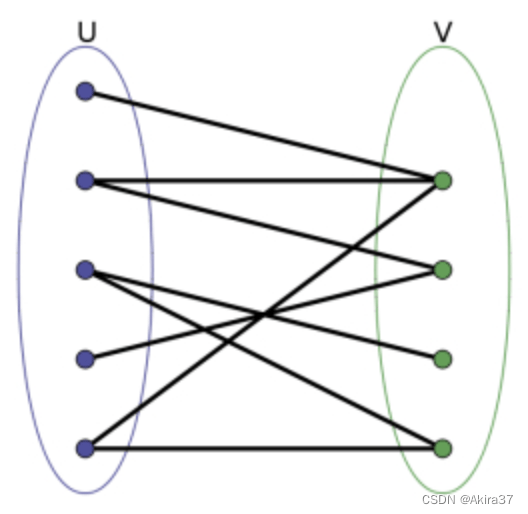
3.6.1 染色法
时间复杂度:O(n+m)
判断是否是二分图
思想:若为二分图,则与黑点相连的点均为白色,与白点相连的点均为黑色(邻接顶点不得同色)
C++
int n; // V: [1 ... n]
int h[N], e[M], ne[M], idx; // 邻接表图
int color[N]; // 每个点的颜色:-1未染色,0白色,1黑色
/* 用dfs给结点u染颜色c,一切顺利返回true,出现冲突则返回false */
bool dfs(int u, int c) {
color[u] = c; // 给结点u染颜色c
for (int i = h[u]; ~i; i = ne[i]) { // 遍历所有从结点u指出的点
int v = e[i];
if (color[v] == -1) { // 若v未染色则将其染与u相反的色(!c)并判定是否冲突
if (!dfs(v, !c)) return false;
} else if (color[v] == c) {
return false; // 若v与u同色则出现冲突
}
}
return true;
}
/* 用染色法判断图是否是二分图 */
bool check() {
memset(color, -1, sizeof color);
for (int i = 1; i <= n; i++) { // 遍历所有顶点,若未染色则染白色并判定是否冲突
if (color[i] == -1) {
if (!dfs(i, 0)) {
return false;
}
}
}
return true;
}3.6.2 匈牙利算法
时间复杂度:最差O(nm),实际运行时间一般远小于O(nm)
用于求二分图的最大匹配数(匹配:某两个点有且只有他们之间有边,与别人无边)
匈牙利算法中只会用到从第1个集合指向第2个集合的边,所以这里只用存一个方向的边。
C++
int n1, n2; // 二分图中两个集合的点数。集合1: [1 ... n1]、集合2: [1 ... n2]
int h[N], e[M], ne[M], idx; // 邻接表图,只存集合1到集合2的边
int match[N]; // match[i] = j表示集合2的点i当前匹配集合1的点j(j=0表示暂无匹配)
bool st[N]; // st[i]标记集合2的点i是否已经被遍历过
/* 寻找与集合1的点u匹配集合2的点,返回是否成功 */
bool find(int u) {
for (int i = h[u]; ~i; i = ne[i]) { // "遍历所有可能"
int v = e[i];
if (!st[v]) {
st[v] = true;
if (match[v] == 0 || find(match[v])) {
match[v] = u;
return true;
}
}
}
return false;
}
/* 求最大匹配数 */
int count_matches() {
int res = 0;
for (int i = 1; i <= n1; i++) { // 依次枚举集合1的每个点去匹配集合2的点
memset(st, false, sizeof st); // 每次重置遍历标记
if (find(i)) {
res++;
}
}
return res;
}3.7 拓扑排序
时间复杂度:O(n+m)
C++
int n; // V: [1 ... n]
int q[N], hh = 0, tt = -1; // 顶点队列,存储拓扑序列
int d[N]; // d[i]存储点i的入度
/* 拓扑排序:将拓扑序列存在队列中 */
bool topo_sort() {
for (int i = 1; i <= n; i++) { // 将所有度为0的点入队
if (d[i] == 0) {
q[++tt] = i;
}
}
while (hh <= tt) {
int t = q[hh++];
for (int i = h[t]; ~i; i = ne[i]) { // 遍历点t的所有出边
int u = e[i]; // 该出边对应的点u
if (--d[u] == 0) {
q[++tt] = u; // 删去该出边并判定:u入度变为0了则入队
}
}
}
return tt = n - 1; // 若所有点都入队了,说明存在拓扑序列;否则不存在拓扑序列
}
/* 输出拓扑序列(若存在) */
void print_topo() {
if (topo_sort()) {
for (int i = 0; i < n; i++) {
printf("%d ", q[i]);
}
puts("");
}
}4 数学
质数、约数、欧拉函数、快速幂、扩展欧几里得算法、高斯消元、组合数
4.1 质数
定义:在大于1的整数中,只包含1和本身这两个约数的数称为质数(素数)
4.1.1 试除法判定质数
时间复杂度:O(\sqrt n)
C++
bool is_prime(int x) {
if (x < 2) return false;
for (int i = 2; i <= x / i; i++) { // 枚举到sqrt(x)
if (x % i == 0) return false;
}
return true;
}Java
public static boolean isPrime(int x) {
if (x < 2) {
return false;
}
for (int i = 2; i <= x / i; i++) {
if (x % i == 0) {
return false;
}
}
return true;
}4.1.2 试除法分解质因数
时间复杂度:O(\sqrt n)
C++
vector<pair<int, int> > primes; // 存储质因数及其个数
void divide(int x) {
for (int i = 2; i <= x / i; i++) // 枚举到sqrt(x)
if (x % i == 0) {
int cnt = 0; // cnt记录质因子i的个数
while (x % i == 0) {
x /= i;
cnt++;
}
primes.push_back({i, cnt});
}
if (x > 1) {
primes.push_back({x, i}); // 原理:x中只包含1个大于sqrt(x)的质因子
}
}Java
public static List<int[]> divide(int x) {
List<int[]> pairs = new ArrayList<>(); // 存储质因数及其个数
for (int i = 2; i <= x / i; i++) {
while (x % i == 0) {
int cnt = 0;
while (x % i == 0) {
x /= i;
cnt++;
}
pairs.add(new int[]{i, cnt});
}
}
if (x > 1) {
pairs.add(new int[]{x, 1}); // x中只包含1个大于sqrt(x)的质因子
}
return pairs;
}4.1.3 筛法求素数表
4.1.3.1 埃氏筛法
时间复杂度:O(n\log\log n)
C++
int primes[N], len; // 存储所有素数
bool st[N]; // st[i]标记数i是否被筛掉
/* 埃氏筛法求[2, n]上所有素数 */
void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (!st[i]) { // 仅遍历未被筛去的数,且只筛它的倍数
primes[len++] = i;
for (int j = i + i; j <= n; j += i) { // 筛去i的倍数,朴素法遍历全部倍数
st[j] = true;
}
}
}
}Java
public static List<Integer> sieveOfEratosthenes(int n) {
List<Integer> primes = new ArrayList<>();
boolean[] st = new boolean[n + 1]; // 标记数i是否被筛掉(非素数)
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes.add(i);
for (int j = i + i; j <= n; j += i) { // 筛去i的倍数,朴素法遍历全部倍数
st[j] = true;
}
}
}
return primes;
}4.1.3.2 线性筛法
时间复杂度:O(n)
核心思想:每个合数只会被其最小质因子筛掉。对于i和素数P_j,若i \bmod P_j=0,且P_j是i的最小质因子,即一定是P_j \cdot i的最小质因子。
C++
int primes[N], len; // 存储所有素数
bool st[N]; // st[i]标记数i是否被筛掉
/* 线性筛法求[2, n]上所有素数 */
void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes[len++] = i;
}
for (int j = 0; primes[j] <= n / i; j++) { // primes[j] * i <= n
st[primes[j] * i] = true; // 每个合数只会被其最小质因子筛掉
if (i % primes[j] == 0) break; // 保证primes[j]一定是primes[j] * i的最小质因子
}
}
}Java
public static List<Integer> getPrimes(int n) {
List<Integer> primes = new ArrayList<>();
boolean[] st = new boolean[n + 1]; // 标记数i是否被筛掉(非素数)
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes.add(i);
}
for (int j = 0; primes.get(j) <= n / i; j++) {
st[i * primes.get(j)] = true;
if (i % primes.get(j) == 0) {
break; // i的最小质因子是primes.get(j),故i * primes.get(j)的最小质因子必为primes.get(j)
}
}
}
return primes;
}4.2 约数
4.2.1 试除法求所有约数
时间复杂度:取决于排序函数,试除的消耗是O(\sqrt n)
C++
/* 求所有约数(去重且递增排序) */
vector<int> get_divisors(int x) {
vector<int> res;
for (int i = 1; i <= x / i; i++) { // 枚举到sqrt(x)
if (x % i == 0) { // 若i为x的约数,则x/i也是x的约数
res.push_back(i);
if (i != x / i) {
res.push_back(x / i); // 不重复存储约数sqrt(x)
}
}
}
sort(res.begin(), res.end());
return res;
}Java
public static List<Integer> getDivisors(int x) {
List<Integer> divisors = new ArrayList<>();
for (int i = 1; i <= x / i; i++) { // 枚举到sqrt(x)
if (x % i == 0) { // 若i为x的约数,则x/i也是x的约数
divisors.add(i);
if (i != x / i) { // 不重复存储约数sqrt(x)
divisors.add(x / i);
}
}
}
divisors.sort(null); // 对约数进行排序
return divisors;
}4.2.2 约数个数、约束之和
设N = p_1^{\alpha_1} p_2^{\alpha_2} \cdots p_k^{\alpha_k},其中p_i是试除法求得的约数(个数为\alpha_i),则
约数个数:
\prod^k\limits_{i=1}(\alpha_i+1)=(\alpha_1+1)(\alpha_2+1)\cdots(\alpha_k+1)约数之和:
\prod^k\limits_{i=1}(\sum^{\alpha_i}\limits_{j=0}p_i^j)=(p_1^0+p_1^1+\cdots+p_1^{\alpha_1})\cdots(p_k^0+p_k^1+\cdots+p_k^{\alpha_k})C++
typedef long long LL;
const int MOD = 1e9 + 7; // 防止结果过大而溢出
int x;
vector<pair<int, int> > primes; // 由试除法分解质因数函数divide()返回的数组,存储约数p_k及其个数a_k
/* 求约数个数 */
LL count_divisors() {
LL cnt = 1;
for (auto prime : primes) {
cnt = cnt * (prime.second + 1) % MOD;
}
return cnt;
}
/* 求约数之和 */
LL sum_divisors() {
LL sum = 1;
for (auto prime: primes) {
int p = prime.first, a = prime.second; // 约数p与指数a
LL t = 1; // 记录p^0+...+p^a
while (a--) {
t = (t * p + 1) % MOD; // 秦九韶算法
}
sum = sum * t % MOD;
}
return sum;
}Java
static final int MOD = 1000000007;
/* 求约数个数 */
public static long countDivisors(int x) {
List<int[]> pairs = Primes.divide(x); // 存储分解所得的质因数及其个数
long cnt = 1;
for (int[] pair : pairs) {
cnt = cnt * (pair[1] + 1) % MOD;
}
return cnt;
}
/* 求约数之和 */
public static long sumDivisors(int x) {
List<int[]> pairs = Primes.divide(x); // 存储分解所得的质因数及其个数
long sum = 1;
for (int[] pair : pairs) {
int p = pair[0], a = pair[1]; // 约数p与指数a
long tmp = 1;
while (a-- > 0) {
tmp = (tmp * p + 1) % MOD; // 秦九韶算法
}
sum = sum * tmp % MOD;
}
return sum;
}4.2.3 欧几里得算法
整除的性质:若d \mid a,\ d \mid b,则d \mid ax+by
欧几里得算法(辗转相除法)求最大公约数:
\gcd(a,b)=\gcd(b,a \bmod b)时间复杂度:O(\log n)
C++
int gcd(int a, int b) {
return b ? gcd(b, a % b) : a; // gcd(a, 0) = a
}Java
public static int gcd(int a, int b) {
return b != 0 ? gcd(b, a % b) : a;
}4.2.4 求最小公倍数
由欧几里得算法可得最小公倍数公式
\text{lcm}(a,b)=\frac{ab}{\gcd(a,b)}C++
int lcm(int a, int b) {
return a / gcd(a, b) * b;
}Java
public static int lcm(int a, int b) {
return a / gcd(a, b) * b;
}4.3 欧拉函数
定义:(1,N)内与N互质的数的个数称为欧拉函数,记为\phi(N)。
求法:若N=p_1^{a_1}p_2^{a_2}\cdots p_m^{a_m} ,则
\phi(N)=N\prod^m\limits_{i=1}(1-\frac1{p_i})特别地,对于质数p,有
\phi(p)=p-1欧拉定理:若a与m互质,即\gcd(a,m)=1,则
a^{\phi(m)}\equiv 1 \pmod m费马小定理:若p为质数,则
a^{\phi(p)}\equiv1\pmod p \Rightarrow a^{p-1}\equiv 1\pmod p \Rightarrow a^p\equiv a\pmod p4.3.1 求欧拉函数
时间复杂度:O(\sqrt n)
C++
int phi(int x) {
int res = x;
for (int i = 2; i <= x / i; i++) // 试除法分解质因数
if (x % i == 0) {
res = res / i * (i - 1); // 化简(1 - 1 / i)所得
while (x % i == 0) {
x /= i;
}
}
if (x > 1) {
res = res / x * (x - 1);
}
return res;
}4.3.2 筛法求欧拉函数表
时间复杂度:O(n)
C++
int primes[N], len; // 存储所有素数
int euler[N]; // euler[x]存储x的欧拉函数
bool st[N]; // st[x]存储x是否被筛掉
/* 线性筛法求[1, n]上所有数的欧拉函数 */
void get_eulers(int n) {
euler[1] = 1; // 规定1与任何数互质
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes[len++] = i;
euler[i] = i - 1; // 若i为质数,则phi(i)=i-1(1~i-1均与i互质)
}
for (int j = 0; primes[j] <= n / i; j++) { // p_j * i <= n
st[primes[j] * i] = true;
if (i % primes[j] == 0) { // 若p_j是i的最小质因子,则一定是p_j * i的最小质因子
euler[primes[j] * i] = euler[i] * primes[j]; // 因此phi(p_j * i)的\prod部分与phi(i)完全相同
break;
}
euler[primes[j] * i] = euler[i] * (primes[j] - 1); // 否则phi(p_j * i) = p_j * phi(i) * (1 - 1 / p_j)
}
}
}4.4 快速幂
求a^k \bmod p,时间复杂度:O(\log k)
思想:
a^k\bmod p=\prod\limits^{\log k}_{i=0}a^{2^i}\bmod p\\ a^{2^{i+1}}\bmod p=(a^{2^i}\bmod p)^2\bmod p核心:求k的二进制表示,即
a^k\bmod p=\prod\limits_{i\in\{i|k[i]=1\}} a^{2^i}\bmod p应用:求模为质数的逆元
逆元的定义:ax\equiv 1\pmod m,a,m互质,则称x为a模m的逆元,记为a^{-1}。
求法:当模为质数p时,由费马小定理得
a^{\phi(p)}\equiv1\pmod p \Rightarrow a^{p-1}\equiv 1\pmod p \Rightarrow a\cdot a^{p-2}=1\pmod p故可得逆元的公式:
a^{-1}=a^{p-2}可用快速幂求得。
C++
typedef long long LL;
/* a^k mod p */
LL qpow(int a, int k, int p) {
LL res = 1, t = a; // t记录a^2^i,其中i>=0,表示逻辑上当前迭代至k的第i位
while (k) {
if (k & 1) {
res = res * t % p; // 当k末位(k[i])为1时,结果乘上a^2^i mod p
}
t = t * t % p; // 更新操作 t <- a^2^(i+1) mod p = (a^2^i mod p)^2 mod p
k >>= 1; // k去掉当前末位,使得逻辑上i++
}
return res;
}Java
/* x^n */
public static double quickMul(double x, long n) {
double res = 1.0;
while (n > 0) {
if (n % 2 == 1) {
res *= x;
}
x *= x;
n /= 2;
}
return res;
}
/* x^n % mod */
public static double quickMul(double x, long n, long mod) {
double res = 1.0;
while (n > 0) {
if (n % 2 == 1) {
res = res * x % mod;
}
x = x * x % mod;
n /= 2;
}
return res;
}
/* 递归表示 */
public static double quickMulRecursion(double x, long n) {
if (n == 0) {
return 1.0;
}
double y = quickMulRecursion(x, n / 2);
return n % 2 == 0 ? y * y : y * y * x;
}4.5 扩展欧几里得算法
裴蜀定理:对于任意正整数a, b,存在非零整数x,y,使得ax+by=\gcd(a,b)。
求通解:设特解x_0,y_0满足ax_0+b_0y=d ①,其中d=\gcd(a,b)。原方程可化为a(x-\frac bd)+b(y+\frac ad)=d②。由①②可得通解为
\left\{\begin{matrix}
x=x_0-\frac bdk\\ y=y_0+\frac adk,
\end{matrix}\right.
,\ k\in \mathbb{Z^+}应用:求解线性同余方程。对于方程ax\equiv b\pmod m,\exist y\in\mathbb{Z^+},ax=my+b\ \xRightarrow{y'=-y} ax+my'=b,该方程有解的充要条件为\gcd(a,m)|b,此时可用扩展欧几里得算法exgcd(a, b, x, y')求得一组特解,进而求得原方程的解。特别地,求a模m的逆元即为b=1的情况。
中国剩余定理:对于两两互质的k个数m_1,m_2,\cdots,m_k,线性同余方程组
\left\{\begin{matrix}
x\equiv a_1\pmod{m_1}\\
x\equiv a_2\pmod{m_2}\\
\vdots \\
x\equiv a_k\pmod{m_k}
\end{matrix}\right.的通解为
x=a_1M_1M_1^{-1}+a_2M_2M_2^{-1}+\cdots+a_kM_kM_k^{-1}其中M=m_1m_2\cdots m_k,M_i=\frac{M}{m_i}\ (i=1,2,\cdots,k),M_i^{-1}为M_i模m_i的逆元,可通过解M_ix\equiv1\pmod{m_i}求得。
C++
/* 求一组x, y特解,满足a*x + b*y = gcd(a, b)。函数返回最大公约数 */
int exgcd(int a, int b, int &x, int &y) { // x, y用引用型
if (!b) { // gcd(a, 0) = a,此时a*x + 0*y = a的通解为(1, 任何数)
x = 1; // 这里传回特解(1, 0)
y = 0;
return a;
}
int d = exgcd(b, a % b, y, x); // 将x、y翻转(便于对比条件),使得b*y + (a mod b)*x = gcd(b, a mod b) = gcd(a, b)
y -= (a / b) * x; // a mod b = a - [a/b]*b,代入上式化简得a*x + b*(y - [a/b]*x) = d,对比条件可知y的变化量!
return d;
}4.6 高斯消元
化增广矩阵为最简行阶梯形矩阵,解n元线性方程组,时间复杂度:O(n^3)
C++
const double eps = 1e-6;
int n;
double a[N][N]; // n*(n+1)的增广矩阵 a[0 ... n-1][0 ... n]
/* 0:有唯一解(此时将增广矩阵化为最简行阶梯形矩阵),1:有无穷多组解,2:无解 */
int gauss() {
int c, r; // 枚举的列、行(同时也记录实际方程个数)
for (c = 0, r = 0; c < n; c++) { // 枚举每一列c,最终化为行阶梯形矩阵
int t = r;
for (int i = r; i < n; i++) { // 寻找绝对值最大的行,记录于t
if (fabs(a[i][c]) > fabs(a[t][c])) {
t = i;
}
}
if (fabs(a[t][c]) < eps) continue; // 若为0则无需消元,跳至下一列
for (int i = c; i <= n; i++) {
swap(a[t][i], a[r][i]); // 将绝对值最大的行t换到最顶端的当前行r
}
for (int i = n; i >= c; i--) {
a[r][i] /= a[r][c]; // 将当前行r同除以该行首a[r][c],使得行r首非零元变成1
}
for (int i = r + 1; i < n; i++) {// 用当前行r将行r首非零元该列下方所有元素消成0
if (fabs(a[i][c]) > eps) { // 若为0则无需再遍历操作该行,节省时间
for (int j = n; j >= c; j--) { // 行i同减行r各列同列元a[r][j]乘以行i首非零元a[i][c](为了消之为0)
a[i][j] -= a[r][j] * a[i][c];
}
}
}
r++; // 完成本列c消元操作后才跳至下一行
}
if (r < n) { // 若化简后的方程个数小于n(最后n-r行系数阵部分全为0,即0行),则有无穷多组解或无解
for (int i = r; i < n; i++) { // 若某行左边为0而右边非0,则直接判无解
if (fabs(a[i][n]) > eps) {
return 2; // 无解
}
}
return 1; // 有无穷多组解
}
for (int i = n - 1; i >= 0; i--) { // 有唯一解则化为最简行阶梯形矩阵,列n所存的即为解
for (int j = i + 1; j < n; j++) { // 同化行阶梯形操作,用各行首非零元将其列上上全部元素消为0
a[i][n] -= a[i][j] * a[j][n];
}
}
return 0; // 有唯一解
}4.7 组合数
组合数\text{C}_n^m(或\text{C}(n,m)、{n \choose m})的定义:
\text{C}_n^m=\frac{n\times(n-1)\times\cdots\times(n-m+1)}{1\times2\times\cdots\times m}=\frac{n!}{(n-m)!m!}\ (m\le n)互补性:
\text{C}_n^m=\text{C}_n^{n-m}递推式:
\text{C}_n^m=\text{C}_{n-1}^m+\text{C}_{n-1}^{m-1}4.7.1 递推法求组合数
适用于处理10^5量级的数据量、1≤m≤n≤2000的情况,时间复杂度:O(n^2)
C++
const int MOD = 1e9 + 7; // 防止结果过大溢出
int c[N][N]; // c[i][j]即为C(i, j),表示从i个不同元素中取j个的方案数
/* 计算C(0, 0) ~ C(N-1, N-1) */
void calc() {
for (int i = 0; i < N; i++) {
for (int j = 0; j <= i; j++) {
if (!j) {
c[i][j] = 1; // 规定“取0个/不取”算作只有1种方案
} else {
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
}
}
}
}4.7.2 通过逆处理逆元的方式求组合数
\text{C}_n^m=n!\cdot((n-m)!)^{-1}\cdot (m!)^{-1},其中((n-m)!)^{-1},(m!)^{-1}分别为(n-m)!,m!模p的逆元,p为质数。由费马小定理得逆元公式a^{-1}=a^{p-2},运用快速幂即可快速求解。
适用于处理10^4量级的数据量、1≤m≤n≤10^5的情况,时间复杂度:O(n\log n)
C++
typedef long long LL; // 预处理时临时防爆int
const int MOD = 1e9 + 7; // 防止结果过大溢出
int fact[N]; // fact[i]存储i的阶乘再取模
int infact[N]; // infact[i]存储fact[i]的模为质数的逆元再取模
/* qpow(a, k, p):快速幂(a^k mod p)模板,用于求模为质数的逆元 */
// 详见4.4
/* 预处理阶乘的余数fact[]和阶乘逆元的余数infact[] */
void init() {
fact[0] = infact[0] = 1; // 0! = 1,1的任何逆元为1
for (int i = 1; i < N; i++) { // 递推求解
fact[i] = (LL)fact[i - 1] * i % MOD;
infact[i] = (LL)infact[i - 1] * qpow(i, MOD - 2, MOD) % MOD;
}
}
/* C(a, b)的值 */
int C(int a, int b) {
return fact[a] * infact[a - b] * infact[b] % MOD;
}4.7.3 Lucas定理
Lucas定理:若p为质数,则对于任意整数1≤p≤m≤n,有
\text{C}_n^m \equiv \text{C}_{n \bmod p}^{m \bmod p}\text{C}_{n/p}^{m/p}\pmod p适用于较低数据量、 1≤m≤n≤10^{18},1≤p≤10^5的情况,时间复杂度:O(\log_p n\cdot p\log p)
C++
typedef long long LL;
/* qpow(a, k, p):快速幂(a^k mod p)模板,用于求模为质数的逆元 */
// 详见4.4
/* 求int型数的组合数C(a, b) */
int C(int a, int b, int p) {
if (a < b) return 0;
LL x = 1, y = 1; // 由最初的定义式,x为分子,y为分母
for (int i = a, j = 1; j <= b; i--, j++) {
x = x * i % p; // x = a! / (a-b)!
y = y * j % p; // y = b!
}
return x * qpow(y, p - 2, p) % p; // 结果即为x * (y的逆元) mod p
}
/* 通过Lucas定理求long long型数的组合数lucas(a, b) */
int lucas(LL a, LL b, int p) {
if (a < p && b < p) return C(a, b, p); // a, b都小于p时用逆元法即可
return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}4.7.4 分解质因数法求组合数
不取模,求出组合数的真实值:
- 筛法求出范围内的所有质数
- 通过组合数定义式
\text{C}_n^m=\frac{n!}{(n-m)!m!}求出每个质因子的次数:n!中p的次数为\frac np + \frac n{p^2} + \frac n{p^3} + \cdots - 用高精度乘法将所有质因子相乘
C++
int n;
int primes[N], len; // 存储所有质数
int sum[N]; // 存储每个质数的次数
bool st[N]; // 存储每个数是否已被筛掉
/* get_primes(n):线性筛法求素数,存至primes[] */
// 详见4.1.3.2
/* 求n!中质因子p的次数:n / p + n / p^2 + n / p^3 + ... */
int get(int n, int p) {
int res = 0;
while (n) {
res += n / p;
n /= p;
}
return res;
}
/* mul(A, b):高精度乘低精度模板 */
// 详见1.3
/* 预处理范围n以内所有质因子,存储每个质因子的个数 */
void init(int a, int b) { // a、b为所求组合数C(a, b)的上下标
get_primes(a);
for (int i = 0; i < len; i++) { // 求每个质因子的次数
int p = primes[i];
sum[i] = get(a, p) - get(a - b, p) - get(b, p); // C(a, b) = a! / ((a - b)! * b!)
}
}
/* 用高精度乘法将所有质因子相乘,存于数组 */
void calc() {
vector<int> res;
res.push_back(1); // 初值为1
for (int i = 0; i < len; i++) {
for (int j = 0; j < sum[i]; j++) { // 乘sum[i]次primes[i]
res = mul(res, primes[i]);
}
}
}4.7.5 卡特兰数
卡特兰数(Catalan Number):C_n=\frac{\text{C}_{2n}^n}{n+1}
C++
int catalan(int n) {
return C(n, 2 * n) / (n + 1)
}
okok